接弦定理の証明、デカルトの探究方法を添えて

【目次】
１．接弦定理
  １－１．定理の解説
２．証明の方針
  ２－１．デカルトの真理探究法の適用
    ２－１－１．高校数学の幾何学の大切さ
    ２－１－２．探究法の復習から
    ２－１－３．第一の規約
    ２－１－４．第二の規約
    ２－１－５．第三の規約
    ２－１－６．第四の規約
    ２－１－７．第二・三の規約と演繹的推論
    ２－１－８．接弦定理における演繹的推論の構成
  ２－２．デカルトの真理探究法の結び
３．接弦定理の証明

数学Ａの教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）では、接弦定理の証明が、接線と弦の作る角が鋭角と直角の場合については丁寧に証明され、鈍角の場合については生徒への問題となっています。

そのため、教科書を読めば接弦定理の証明は概ね理解することができると思いますが、接弦定理の証明に必要となる「円の中心点と接点を結ぶ直線は接線と垂直に交わる」ことと「円周角の定理」が教科書では証明されていないので、本記事で接弦定理の証明を行うために、過去数記事にて準備を行ってきました。

以下の解説中でも必要な個所で参照を載せようと思いますが、
円と直線の距離と位置関係、特に交点、接点、接線について
円周角の定理とその逆の証明
の２記事となります。

くわえて、【証明の方針】では、デカルトの真理探究法の活用、適用の実際も例示します。

接弦定理

それでは、まず、接弦定理とは教科書によると、

【接弦定理】

接線と弦の作る角
円\(O\)の弦\(AB\)と、その端点\(A\)における接線\(AT\)が作る角\(\angle BAT\)は、その角の内部に含まれる弧\(AB\)に対する円周角\(\angle ACB\)に等しい。

図１：接弦定理（弦と接線と弧と円周角の関係）

となります。

とても明確に書いてあるので、順番を追って丁寧に読めば理解できると思いますが、「円」「弦」「接線」「弧」「円周角」などの用語の意味を忘れている場合には、少し混乱する恐れがあるので、きちんと定理の解説から始めたいと思います。

定理の解説

まず、そもそも接弦定理は、その名前の通りに、円の接線と弦についての定理です。

それも、第一に、円の弦の端点が接線の接点と一致している場合についての定理です。つまり、円の弦の端点に接線を引くか、円の接線の接点から弦を引くか、というどちらかの場合の定理というわけです。

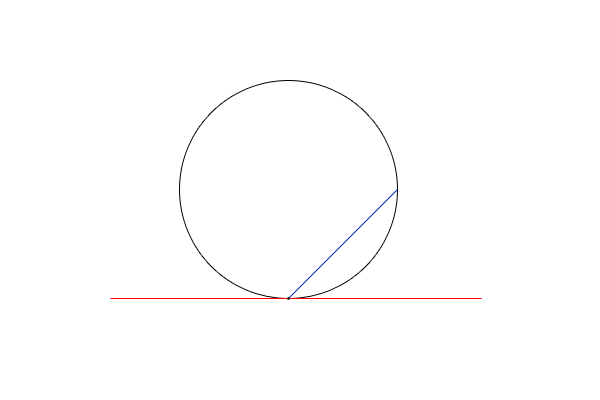
図２：円、弦、接線

その上で、第二に、円の接線と弦の作る角に着目をします。ちなみに、接線と弦があったら、弦から時計回りと反時計回りの二つの角があるわけですが、どちらの角に着目するのか気になる方もいるかもしれませんが、どちらの角に着目しても良いのです。

このことから、接弦定理のことを教科書では、「接線と弦の作る角」についての定理と呼んでいるわけです。

そして、さらに定理を読み進めると、円周角と接線と弦の作る角が等しいことが結論となっていることが分かります。しかし、この際にも、弦によって二分割された円のどちらの側の円周角なのかが問題になります。円周角は、弦のどちらの側にあるかによって角度が変わるので、この場合は、どちらでも良いというわけにはいきません。

そこで、まず、思い出すべきは、円周角は弦ではなく、弧によって指定されるということです（参照：円周角の定理とその逆の証明）。

したがって、教科書でも「接線と弦の作る角の内部に含まれる弧に対する円周角」として円周角を指定しているわけです。つまり、接線と弦の作る角の内部にあるか、外部にあるかによって、弦に対して二つある弧のどちらかを指定しています。

簡単にまとめると、「接線と弦の作る角」をどちらの角に着目したかによって、その弦をまたいだ反対側の円周角と等しくなります。

定理の流れとしては、円の弦と接線が決まる、接線と弦の作る角が決まる、その角に対する弧と円周角が決まる、そして、接線と弦の作る角と円周角が等しい、という順序で考えが進みます。

証明の方針

デカルトの真理探究法の適用

それではこの記事では良い機会なので一度、本サイトの方針（参照：トップページ：合理的に物事を考える具体的な方法）の通りに、明示的に合理的に物事を考える方法：デカルトの真理探究法を当てはめる形で、証明の方針を考えてみたいと思います。

高校数学の幾何学の大切さ

ちなみに、現代思想の基礎を築いたデカルトも、現代数学の基礎を築いたヒルベルトも、近代や現代科学のエポックメイキングを起こしたニュートンやアインシュタインも、ユークリッドの原論の幾何学、つまり、この高校数学の幾何学の研究を大きな土台の一つにしてきたことは間違いありません。数学や科学に興味のある学生は、若いうちに彼らの考え方や研究の仕方を学んでみることが将来にとても役立つと思います。

したがって、高校数学の幾何学はもちろん馬鹿にできない分野でありますし、ここで行うようなアプローチで学ぶことを面白い試みと捉える方もいるかもしれませんが、実際の解説が上手くできているかできていないかは別にして、当たり前のこととして捉える方たちも多くいるはずです。

ただし、皆が当たり前のように行っているけれども、実際に目の前で解説されることの少ないこともよくあるものです。私自身はこのような幾何学教育を明示的に受けたことはなかったと思いますが、いや、不真面目な学生であった私が授業を聞いていなかっただけのような気も大いにします。

探究法の復習から

それでは、話を元に戻して、照らし合わせやすいように再掲しておくと、簡単に表現したデカルトの方法が、

１．注意深く疑問を持って考え、自分が本当に正しいと思うことだけを受け入れる。
２．より分かりやすいように、できるだけ多くそして必要なだけの小さな要素に分解する。
３．正しいことを単純な要素から複雑な要素まで順序立てて一つづつ考える、少なくとも順序を想定する。
４．以上のすべての場合に、全体を見直し、すべてを列挙して何も見落とさない。

でした。注意事項など、詳しくは上述のリンクページをご覧ください。

第一の規約

第一の規約は、出発点であり第二～四の規約を支える重要な基礎でもあります。

まず、第一の規約に基づいて「接弦定理」が正しいかどうか、疑問を持って考えてみます。そうすると、「接弦定理」が結論として「接線と弦の作る角」と「円周角」が等しいことを言っていることが分かります。

それならば、コンパス、定規、分度器等を使って作図してみるのも自分が本当に正しいと思えるかの確認になります。とりあえず、それで正しそうであるならば、どうして正しいのか根拠を探す証明へと進んでいきます。

第二の規約

第二の規約は、その根拠を探すための手段になっています。より分かりやすいように、どこまで小さな要素に分解するべきかが難しいところですが、まずはできるだけ多く、分解してみましょう。

そうすると、一見すると「円」「接線」「弦」「接点」「角」「弧」「円周角」あたりがこの「接弦定理」を構成している主要な要素としてすぐに思い付きます。

ただし、ここで終わらずに第一の規約にある通り疑問を持って、さらにできるだけ多くの要素に分けていきましょう。少しばかり不要なほど分解してしまっても後から除外すれば良く、それぐらいが丁度良いと思います。

すると、「円」は「中心点」「半径」「円周」、「接線」「弦」は「直線」、「接点」は「点」で構成されていることが分かります。つまり、逆に言えば、分解することができます。それでは、例えば「接線」「弦」と「直線」の違いはどこから来るでしょうか？

第三の規約

そこで、第三の規約を用います。正しいことを単純な要素から複雑な要素まで順序立てて一つづつ考えてみましょう。

つまり、それは、「直線」という単純な要素が「円周」と接する場合に、より複雑な要素である「接線」となると考えれば良いわけです。

同じように、「点」は「円周」と「接線」の交点の場合に「接点」となります。

「角」は、二つの「直線」とその交点で構成されています。「弧」は、「円周」の部分です。

そこで、「円周角」は、「弧」の端点を通り端点でない円周の一点で交わる二つの「直線」のなす「角」となります。

第四の規約

ここで、一度、第四の規約を守っているか確認してみましょう。つまり、「接弦定理」を構成しているすべての要素について、すべてを列挙して何も見落としていないかです。そうすると「円」「接線」「弦」「接点」「角」「弧」「円周角」の中で、「弦」の分解を忘れていました。

「弦」は、「弧」の端点を結ぶ直線の部分、つまり線分と言えます。これで、見落としをなくすことができました。

第二・三の規約と演繹的推論

それでは、ここで再び第一の規約に戻りましょう。つまり、分解も列挙もした、それではこれらの要素を用いて、結論である「接線と弦の作る角」と「円周角」が等しいことをどう証明すればよいのか？、と疑問を持ちます。

そこで、よく考えると、少し一般論に踏み込みますが、命題や定理というのは、ここまで分解してきた要素の組合せ、それらの関係を表現しているものだと気付きます。例えば、接弦定理は「円」「接線」「弦」「接点」「角」「弧」「円周角」という要素において、「接線と弦の作る角」と「円周角」という要素の大きさが等しいという関係を表しています。

そしてそれはつまり、より単純な命題であれば、単純な要素と単純な関係で構成され、より複雑な命題であれば、複雑な要素と複雑な関係で構成されていると分かります。例えば、二直線の交点は一点のみであるという命題と、接弦定理では、やはり、その要素の複雑さも要素間の関係の複雑さも違います。

さらに、よく考えると、「直線」を使って「接線」を定義したように、複雑な要素は単純な要素によって定義されましたが、同様に、複雑な命題は、単純な命題を組み合わせて使うことで、その正しさを証明できると気付きます。例えば、平行線の錯角が等しいという命題を２回使うことで、三角形の内角の和が\(180^\circ\)と証明できるようにです。（参照：円と直線の距離と位置関係、特に交点、接点、接線について：点と直線についての導入：図７：三角形の内角の和）

そうすると、ここまでは第三の規約の「単純な要素から複雑な要素」の要素という言葉に幾何学的な対象を当てはめて用いてきましたが、ここからは、すでに分解をした要素の関係で構成される命題を当てはめて考えてみましょう。

つまり、第三の規約を、「正しいことを単純な命題から複雑な命題まで順序立てて一つづつ考える、少なくとも順序を想定する」、と読むわけです。

ちなみに、第二の規約も、要素を命題と読み替えることができます。「より分かりやすいように、できるだけ多くそして必要なだけの小さな命題に分解する」、とです。実際、要素という言葉は分かりやすくするための意訳で、本来のデカルトの意図はこの意味に近いのです。

ただし、さらに詳しく言うと、ここでの命題には二種類あります。通常は条件と呼ばれる命題と、普通の意味での命題です。

例えば、「接線」は、「直線と円が接する」という命題を真とした場合の「直線」ということになります。このような命題を通常は、条件と言います。つまり、この「直線」を使って「接線」を定義した場合のように、定義とは、条件による限定と捉え直すことができます。（参照：必要条件と十分条件について：条件とは）

一方で、「円の中心と接点を結ぶ直線は接線と垂直に交わる」という命題のように、ある条件の元で常に正しいことを普通の意味で、命題や定理と呼びます。

つまり、第二の規約は、できるだけ多くそして必要なだけの小さな条件や命題に分解していく、とも言い換えられるのです。ちなみに、条件も命題も高校数学Ⅰで学ぶ内容ですが、このような応用をするには理解を深めておく必要があります（参照：命題について）。

ここまで来ると、新たな視点として、命題や定理の証明とは、分解した一般的で単純な要素の単純な命題の正しさから、条件を付けて少し特殊で複雑な要素の少し複雑な命題を順序立てて一つづつ証明していくことである、と分かります。

ちなみに、このように正しい命題から正しい命題を次々と導き出していく考え方を、演繹的推論と言います。

そこで、接弦定理の話に戻ると、接弦定理とは一般的なすべての二つの組の角の中でも、複雑な要素が複雑な関係で縛られた特殊な条件を満たす場合に、その特別な二つの組の角が等しいという関係が成り立つ命題である、という視点を持てます。もちろん、一般的なすべての二つの組の角が必ずしも等しくないということが前提としてあります。

つまり、接弦定理をどう証明すれば良いか？というと、ここまで分解してきた単純な要素たちに成り立つ条件や命題（第二の規約）から出発して、この複雑な接弦定理に到達するまで、条件や命題をできるだけ順序立てて一つづつ（第三の規約）すべて列挙しながら（第四の規約）証明して行けば良いのです。

接弦定理における演繹的推論の構成

念のため、小さな要素たちから具体的にすべて列挙し直すとおおまかに、
「点」「直線」「角」「中心点」「半径」「円周」「円」「接線」「接点」「弧」「弦」「円周角」
という順番に定義を行っていくことができそうです。

そして、これらの要素たちの間に成立する命題は、すべてを一から列挙するとあまりに長くなるので、大まかには以下の①と②の参照ページに書いてありますが、詳しくは、高校数学の範囲に重なる「ユークリッドの原論」や、高校数学とは言えないですがヒルベルトの「幾何学基礎論」などを読んでみてください。

ちなみに、「ユークリッドの原論」やニュートンの「プリンキピア」などに若いうちに触れて、早いうちにほとんどの有用な学問というものが雑多の知識ではなく、このように原理から体系付けられた演繹的推論を骨格としているということに合点が行くと、将来の勉強がとても効率的になると思います。程度の差はあれ、それは理系文系に限らないことです。

つまり、考える必要のある本当に大切なことはとても少ない、それを抑えてしまえばとても楽なんだという感覚です。

すぐ脱線してしまいますが、再び接弦定理に話を戻して、そうして、「点」と「直線」の関係、「直線」と「直線」の関係、、などなどを経て、接弦定理の直前の根拠になりそうな「接線」や「弦」に関係している命題は、

①「接線」と「円」の重要な関係として、すでに一度触れた「円の中心と接点を結ぶ直線は接線と垂直に交わる」という命題が成り立ちます（参照：円と直線の距離と位置関係、特に交点、接点、接線について）。成り立つことを知らない場合は、成り立ちそうだから証明してみよう、という考えの流れです。

②「弦」と「弧」と「円周角」の重要な関係として、円周角の定理が成り立ちます（参照：円周角の定理とその逆の証明）。これも成り立つことを知らない場合は、成り立ちそうだから証明してみよう、という考えの流れです。

③そこで、円周角の大きさは弧の長さによって決まります。逆も真です。

④円周角と「接線と弦の作る角」が等しいのであれば、「接線と弦の作る角」と弧の長さにも同様の関係が成立するはずです。
たしかに、「接線と弦の作る角」によって弧の長さは決まります。

⑤つまり、「接線と弦の作る角」の大きさに条件を付ければ、弧の長さと円周角が決まるはずです。

⑥特に、「接線と弦の作る角」の大きさが\(90^\circ\)であれば、①より弦は円の中心点を通り、②を合わせて考えると、円周角も\(90^\circ\)でこの場合は、接弦定理が成り立ちそうです。

⑦この「接線と弦の作る角」の大きさが\(90^\circ\)を境にして、「接線と弦の作る角」と円周角は鋭角と鈍角に分かれるので、綺麗な場合分けができそうです。

そして、以上の列挙を総合すると、「接線と弦の作る角」の大きさを\(90^\circ\)、鋭角、鈍角という条件で場合分けし、概ね①と②を用いて証明できないかという方針ができます。

デカルトの真理探究法の結び

デカルトの真理探究法の活用事例は、これで終了です。どこまで深堀するか、あるいは、若干の修正を行うか、の調整が大切になりますが、ここで示した作業は、問題解決が必要となる様々な場面への応用が可能です。デカルトの仕事が現代社会にどれだけの影響を与え、さらにどこまで発展しているかは、学問の歴史や科学史を学ぶ必要があります。

もちろん、基本的な計算や定理に習熟した上で、大学受験の問題解決にも活躍するでしょう。ただ、大学受験の問題は、深堀する必要はなく、さらっと浅堀して解けなければ、恐らく、基本の反復練習や定理の理解が足りないだけだと思います。あまり価値のない問題の解決のみに時間を浪費せず、教科書の理解のためにこのような思考法は活用した方が有意義でしょう。

この接弦定理の証明も「円の中心と接点を結ぶ直線は接線と垂直に交わる」と「円周角の定理」の成立を前提とすれば、分解するのは「円」「接線」「弦」「接点」「弧」「円周角」あたりまでで十分なのです。ただ、デカルトの探究法のそれなりの理解を促すために必要と思われるところまで深堀をしました。

接弦定理の証明

それでは、以上の方針に基づいて証明を行いたいと思います。

【証明】

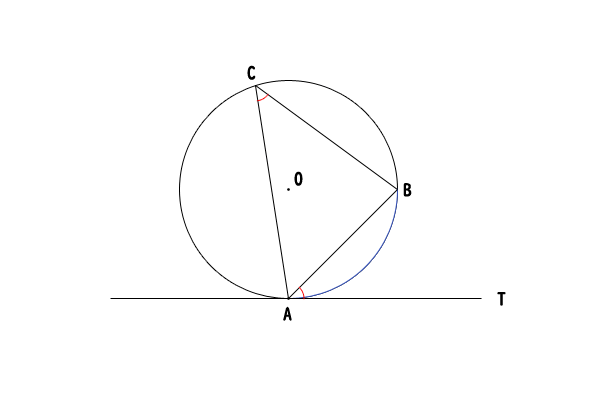
図３：図１を再掲

それでは、接線と弦の作る角\(\angle BAT\)の角度が\(90^\circ\)、鋭角、鈍角の順番に証明を行っていきます。

①\(\angle BAT = 90^\circ\)の場合

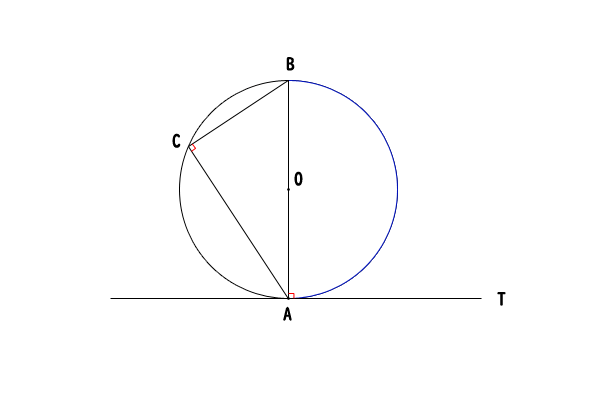
図４：\(\angle BAT = 90^\circ\)の場合

今、接点\(A\)を通り、接線\(AT\)に垂直な直線\(AB\)を引きます。

仮に、直線\(AB\)が円の中心点\(O\)を通らないとすると、直線と直線の位置関係は一致するか、一点で交わるか、平行かの３通りしかないので、直線\(AO\)とは、点\(A\)で交わり、点\(O\)で交わらないので、点\(A\)の一点のみで交わる異なる直線であることが分かります。

すると、接線\(AT\)と点\(A\)においてなす角は、直線\(AB\)と直線\(AO\)で異なることになります。

しかしながら、「円の中心と接点を結ぶ直線は接線と垂直に交わる」（参照：円と直線の距離と位置関係、特に交点、接点、接線について）より、直線\(AO\)も接線\(AT\)の垂線となるのでこれは矛盾します。

したがって、直線\(AB\)が円の中心点\(O\)を通ることが分かりました。

そうすると、弦\(AB\)は円の中心点\(O\)を通るので、円周角の定理（参照：円周角の定理とその逆の証明）より、その円周角\(\angle ACB\)は\(90^\circ\)となります。

以上より、\(\angle BAT = \angle ACB = 90^\circ\)が分かりました。

②\(\angle BAT \lt 90^\circ\)の場合

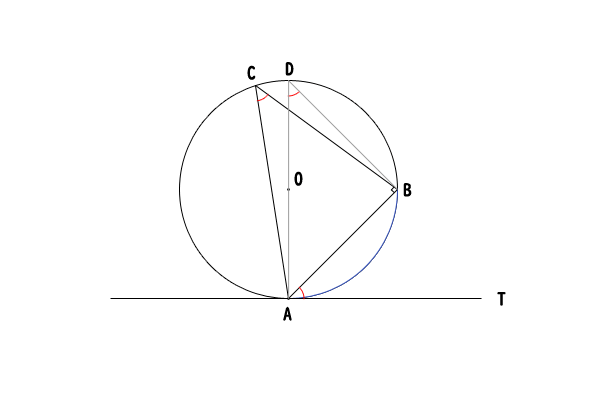
図５：\(\angle BAT\)が鋭角の場合

弦\(AB\)とは別に、補助線として①の場合と同様に、接線\(AT\)に垂直に弦\(AD\)を引くと弦\(AD\)は円の中心点\(O\)を通ります。

したがって、円周角の定理より、\(\angle ABD = 90^\circ\)が成り立ちます。

そうすると、三角形\(ABD\)は直角三角形なので、\(\angle ADB = 90^\circ – \angle BAD\)が成り立ちます。

一方、弦\(AD\)は接線\(AT\)の垂線なので、\(90^\circ = \angle DAT = \angle BAD + \angle BAT\)より、\(\angle BAT = 90^\circ – \angle BAD\)が成り立ちます。

したがって、\(\angle ADB = \angle BAT\)と分かります。

ここで、弧\(AB\)に対する円周角の定理より、\(\angle ACB = \angle ADB\)より、\(\angle ACB = \angle BAT\)が分かりました。

③\(\angle BAT \gt 90^\circ\)の場合

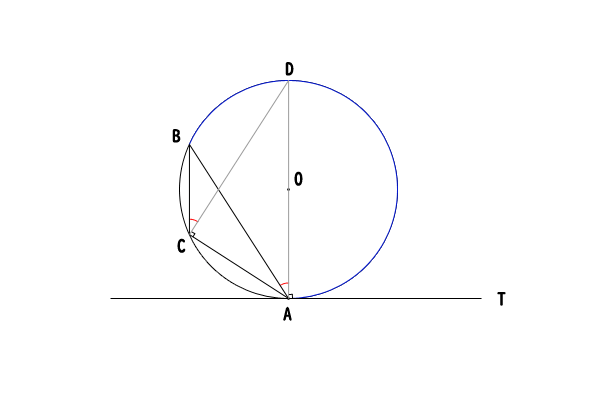
図６：\(\angle BAT\)が鈍角の場合

②と同様に弦\(AB\)とは別に、補助線として接線\(AT\)に垂直に弦\(AD\)を引くと弦\(AD\)は円の中心点\(O\)を通ります。

そうすると、

\[\angle BAT = \angle BAD + \angle DAT \tag{1}\]

\[\angle BCA = \angle DCB + \angle DCA \tag{2}\]

が成り立ちます。

ここで、弦\(AD\)は接線\(AT\)への垂線なので、\(\angle DAT = 90^\circ\)が成り立ちます。

一方、弧\(AD\)に円周角の定理を適用すると、\(\angle DCA = 90^\circ\)が成り立ちます。

さらに、弧\(BD\)に対して円周角の定理を適用すると、\(\angle BAD = \angle DCB\)が成り立ちます。

したがって、これらと式（１）（２）により、\(\angle BAT = \angle BCA\)が分かりました。□

公開日：２０１９年１１月０６日
修正日：ー