方べきの定理とその逆の証明

【目次】
０．はじめに
１．方べきの定理
２．方べきの定理の逆
　　２－１．四角形が円に内接する条件
　　２－２．接弦定理の逆

はじめに

方べきの定理とその逆の証明は、細かく根拠をたどるとそれなりに複雑で、高校数学の教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）では、恐らく掲載できる文章量が限られているため、初めて高校数学を学習する生徒にとってはその行間を埋めて読むには難しい内容だと思います。

そこで、今回は方べきの定理とその逆をきちんと根拠を明示しながら丁寧に証明していきたいと思います。ちなみに、その過程で四角形が円に内接する条件、接弦定理の逆、なども証明します。

方べきの定理

それでは、まずは方べきの定理の証明を行いたいと思いますが、教科書では方べきの定理を場合分けして提示していますが、ここでは、定理自体は一つにまとめて、証明のみを場合分けして行いたいと思います。その方が見通し良く理解しやすいのではないかと思います。

その前に定理を簡単に表現するために、「方べき」の定義を行います。

【定義：方べき】
円$O$とその円上にない点$P$について、点$P$と円$O$を通る直線$l$をとり、円$O$と直線$l$の交点を$A,B$としたときに、$PA \cdot PB$の値を方べきと呼ぶ。ただし、交点が一つしかないときは、つまりその接点を$T$として$PT^{2}$の値を方べきと呼ぶ。

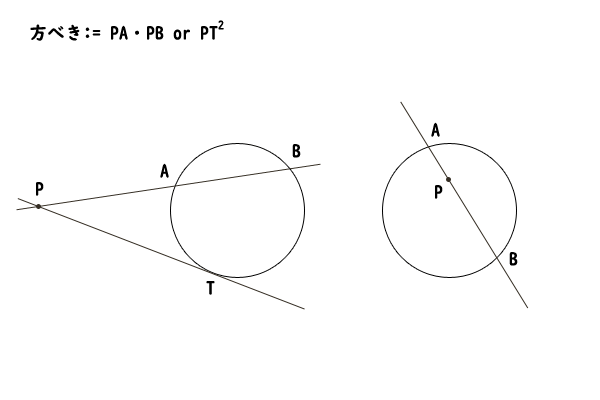
図１：方べきの定義

【方べきの定理】
円$O$とその円上にないある点$P$について、点$P$と円$O$を通る直線の方べきは一定である。

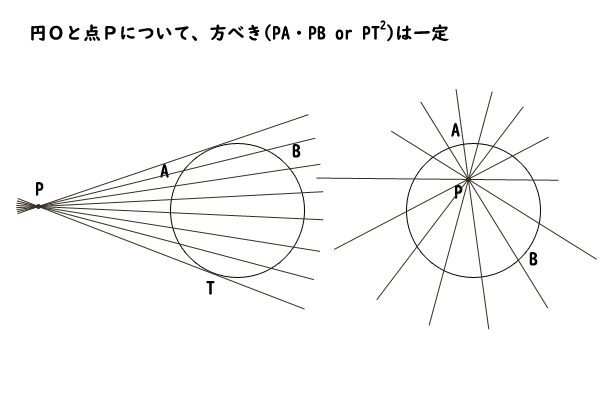
図２：方べきの定理

注意：【方べきの定理】を前提とすると、円$O$に対する点$P$の位置によって方べきは一意に定まるので、その語用は、教科書にもある通り、点$P$の円$O$に関する方べきというように使います。

【証明】
始めに、点$P$と円$O$を通る任意の直線$l$と直線$m$を取ります。

仮に、任意の直線$l$と直線$m$の方べきが等しければ、直線$l$の方べきを数値$A$とすると、直線$m$は点$P$と円$O$を通る任意の直線なので、点$P$と円$O$を通る任意の（すべての）直線の方べきが数値$A$であることが言え、それはつまり、点$P$と円$O$を通るすべての直線の方べきが一定であることになります。

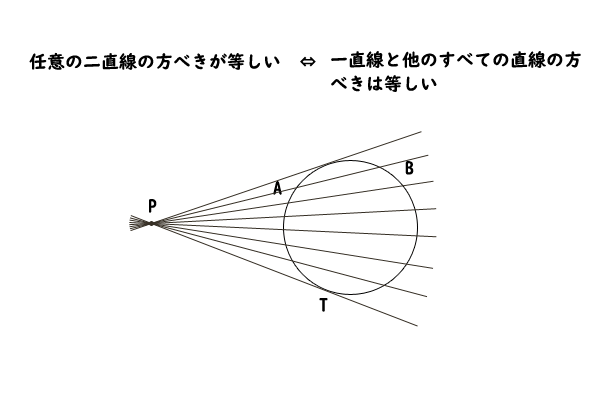
図３：方べきが一定の説明

したがって、点$P$と円$O$を通る任意の直線$l$と直線$m$を取り、互いの方べきが等しいことを示すことができれば、定理の証明は十分に満たされると分かります。

それでは、点$P$と円$O$を通る任意の直線$l$と直線$m$を取り、互いの方べきが等しいことを示しましょう。

そのためには、点$P$が円$O$の①中にあるか②外にあるか、さらに外にある場合には直線$l$と直線$m$の交点が②－①共に２つある、②－②片方が２つありもう一方が１つしかない、②－③共に１つしかない、で場合分けして考えます。

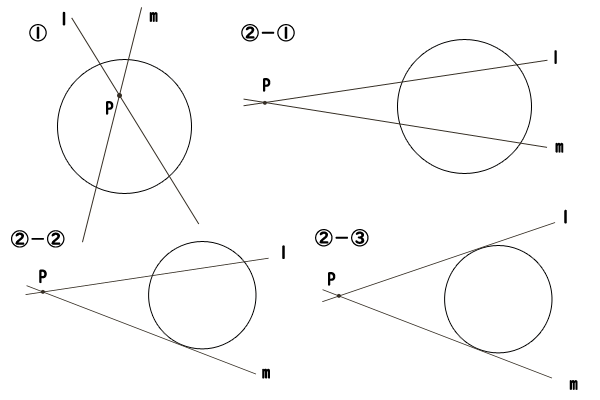
図４：方べきの定理の場合分け

①：

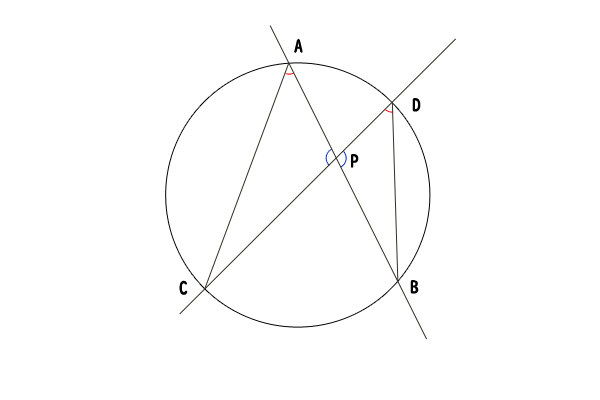
図５：点$P$が円$O$の中にある場合

点$P$が円$O$の中にある場合には、円の中にある一点を通る直線は必ず円と２点で交わるので、円$O$と直線$l$の交点を点$A,B$、円$O$と直線$m$の交点を点$C,D$とします。ただし、時計回りに$A,D,B,C$の並びになるように名付けます。

$\angle APC$と$\angle DPB$は対頂角より等しく、$\angle CAP$と$\angle BDP$は円周角より等しいので、三角形$CAP$と三角形$BDP$は相似になります。したがって、$PA:PC = PD:PB$が成り立ち、$PA\cdot PB = PC\cdot PD$が示せました。

②－①：

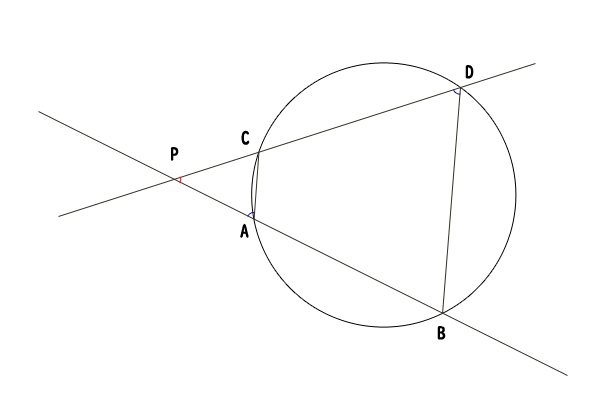
図６：点$P$が円$O$の外にあって、直線$l$と直線$m$が共に円$O$と２点で交わる場合

点$P$が円$O$の外にある場合には、円と直線の交点は２つか１つかの二通りがあるので（参照：円と直線の距離と位置関係、特に交点、接点、接線について）、まずは、直線$l$と直線$m$が共に円$O$と２点で交わる場合を考えましょう。

先ほどと同様に円$O$と直線$l$の交点を点$A,B$、円$O$と直線$m$の交点を点$C,D$とします。ただし、時計回りに$A,C,D,B$の並びになるように名付けます。

三角形$PAC$と三角形$PDB$について、$\angle DPB$は共通であり、$\angle PAC$は円に内接する四角形$ABDC$の外角なので$\angle PAC = \angle BDP$であり、三角形$PAC$と三角形$PDB$は相似であることが分かりました。ちなみに、円に内接する四角形の外角についての法則は、円周角と中心角の関係から四角形の対角の和が$180^{\circ}$であることを導くことで示せます。

したがって、三角形$PAC$と三角形$PDB$が相似なので、$PA:PC = PD:PB$が成り立ち、$PA\cdot PB = PC\cdot PD$が示せました。

②－②：

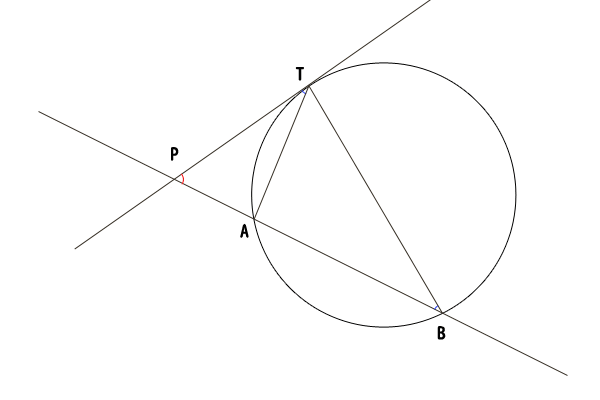
図７：点$P$が円$O$の外にあって、一つの直線が円$O$と２点で交わり、もう一つの直線が円$O$と１点で交わる場合

次に、点$P$が円$O$の外にある場合で、一つの直線が円$O$と２点で交わり、もう一つの直線が円$O$と１点で交わるときを考えましょう。

先ほどと同様に円$O$と直線$l$の交点を点$A,B$とします。そして、円$O$と直線$m$の接点を点$T$とします。ただし、ここでは時計回りに$A,T,B$の並びになる場合のみを考えます。$A,B,T$の並びの場合も同様に考えられます。

三角形$PAT$と三角形$PTB$について、$\angle TPB$は共通であり、接弦定理（参照：接弦定理の証明、デカルトの探究方法を添えて）より$\angle PTA = \angle PBT$であり、三角形$PAT$と三角形$PTB$は相似であることが分かりました。したがって、$PA:PT = PT:PB$が成り立ち、$PA\cdot PB = PT^{2}$が示せました。

②－③：

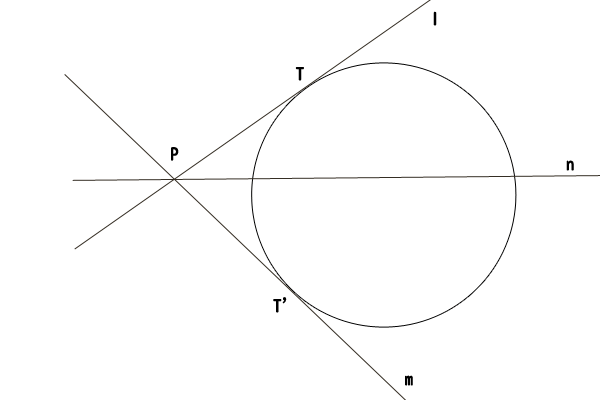
図８：点$P$が円$O$の外にあって、点$P$を通る二つの直線が円$O$と共に１点で交わる場合

最後に、点$P$が円$O$の外にある場合で、点$P$を通る二つの直線が円$O$と共に１点で交わるときを考えましょう。

つまり、直線$l$と直線$m$が共に円$O$の接線となっている場合ですが、円$O$と２点で交わる直線$n$を取れば、上記の②－②一つの直線が円$O$と２点で交わり、もう一つの直線が円$O$と１点で交わる場合の考察により、直線$l$の方べきは直線$n$の方べきと等しく、直線$n$の方べきは直線$m$の方べきと等しいので、直線$l$と直線$m$の方べきが等しいことが分かります。

あるいは、直線$l$と直線$m$が共に円$O$の接線となっていることから、一点を通って円に接する二つの直線の性質により、その接点を$T,T^{‘}$として、$PT=PT^{‘}$が成り立つので、$PT^{2}={PT^{‘}}^{2}$と方べきが等しいことを導くこともできます。一点を通って円に接する二つの直線の性質$PT=PT^{‘}$については、円$O$の中心点を点$C$として三角形$PTC$と三角形$PT^{‘}C$が合同であることから導きます。（先ほど紹介した円と直線の距離と位置関係、特に交点、接点、接線についてを参考にしてみて下さい。）

以上で、円$O$とその円上にないある点$P$について、すべての場合において点$P$と円$O$を通る直線の方べきは一定であることが示せました。□

方べきの定理の逆

それでは、次に、方べきの定理の逆の証明を行いたいと思います。

【方べきの定理の逆】
点$P$を通る二直線$l,m$上にそれぞれ点$A,B$と点$C,D$があり、①点$A,B$と点$C,D$が共に点$P$を挟んでいるとき、あるいは、②点$A,B$と点$C,D$が共に点$P$を挟んでいないときに、$PA\cdot PB = PC\cdot PD$が成り立つならば、点$A,B,C,D$はただ一つの円周上にある。
ただし、後者の点$A,B$と点$C,D$が共に点$P$を挟んでいない場合に点$A,B$と点$C,D$は、②－Ⓐ点$P$とは異なる同一点$A=B=T$あるいは$C=D=T^{‘}$のいずれか一方でも良く、その場合に点$T$や$T^{‘}$は接点である。
さらに、②－Ⓑ共に同一点$T,T^{‘}$である場合には、点$T$と$T^{‘}$が接点となるただ一つの円がある。

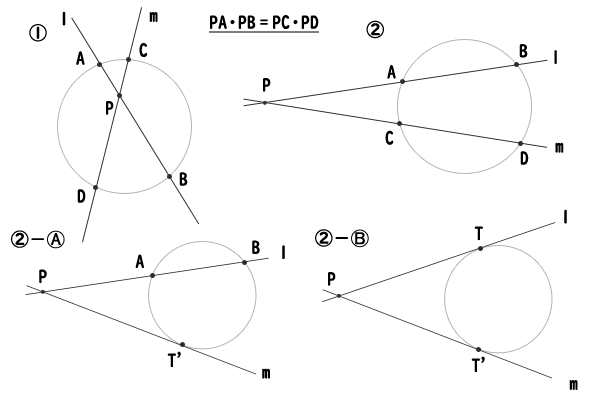
図９：方べきの定理の逆

【解説】
方べきの定理は、円$O$とその円上にないある点$P$について、点$P$と円$O$を通る直線の方べきは一定であることでしたが、その逆は、点$P$に対する仮の方べきが等しければ、点$A,B,C,D$がただ一つの円周上にあることを主張します。ただし、仮の方べきが等しい他の直線$n$の点$E,F$を取ったときに、点$A,B,C,D$で定まる円周上に点$E,F$があることまでは言えないことに注意が必要です。点$A,B,E,F$と点$C,D,E,F$によってそれぞれただ一つの円が定まることが言えるまでです。点$A,B,C,D$、点$A,B,E,F$、点$C,D,E,F$によって定まる各円が一致しているわけではありません。

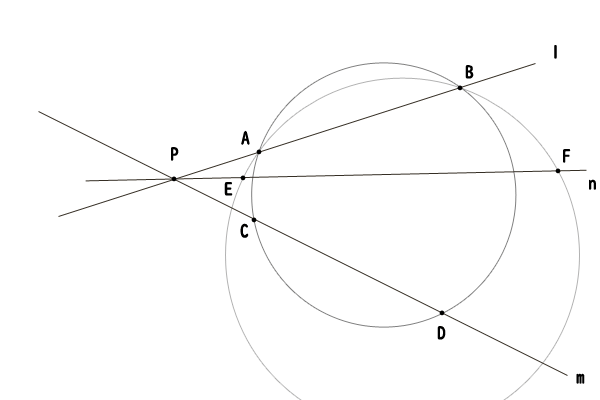
図１０：方べきの定理の逆の解説

【証明】
①：

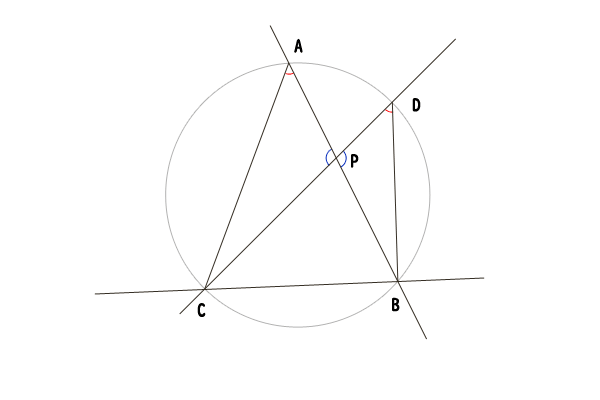
図１１：点$A,B$と点$C,D$が共に点$P$を挟んでいる場合

それでは、まず点$A,B$と点$C,D$が共に点$P$を挟んでいる場合から証明しましょう。ただし、時計回りに$A,D,B,C$の並びになる場合のみをここでは証明します。

三角形$APC$と三角形$DPB$について、対頂角は等しいので$\angle APC=\angle DPB$であり、$PA\cdot PB = PC\cdot PD$より、$PA:PD = PC:PB$なので、三角形$APC$と三角形$DPB$は相似であることが分かります。したがって、$\angle CAB = \angle CDB$であり、くわえて直線$CB$に対して点$A,D$は同じ側にあるので、円周角の定理の逆（参照：円周角の定理とその逆の証明：円周角の定理の逆）より、点$A,D,B,C$がただ一つの円周上にあることを示せました。

②：

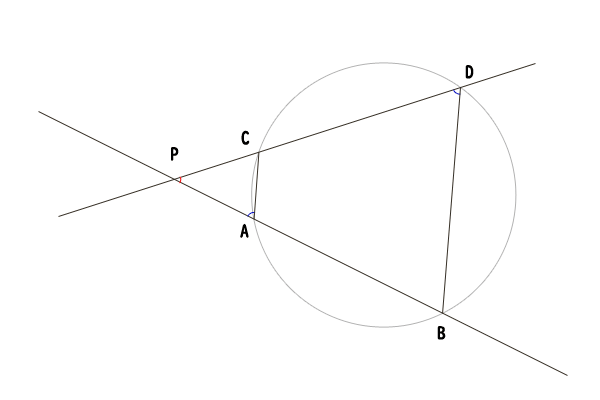
図１２：点$A,B$と点$C,D$が共に点$P$を挟んでいない場合

次に、点$A,B$と点$C,D$が共に点$P$を挟んでいない場合を証明しましょう。ただし、時計回りに$A,C,D,B$の並びになる場合のみをここでは証明します。

三角形$APC$と三角形$DPB$について、共通の角なので$\angle APC=\angle DPB$であり、$PA\cdot PB = PC\cdot PD$より、$PA:PD = PC:PB$なので、三角形$APC$と三角形$DPB$は相似であることが分かります。したがって、$\angle PAC = \angle PDB$であり、四角形$ACDB$において内角$\angle CDB$が、その対角の外角$\angle PAC$に等しいことから（四角形が円に内接する条件は下記で証明します）、点$A,D,B,C$がただ一つの円周上にあることを示せました。

ここで、後付けですが四角形が円に内接する条件、「一つの内角が、その対角の外角に等しい。（教科書より引用）」をきちんと証明しておきましょう。つまり、四角形の一つの内角が、その対角の外角に等しければ、四角形はただ一つの円周上にあることを示します。

《四角形が円に内接する条件の証明開始》
円周角の定理の逆の証明で示した通り、三角形の外接円はただ一つに定まります。したがって、三角形$CAB$と三角形$CDB$の外接円をそれぞれ円$O,O^{‘}$とします。

円$O$上の弦$CB$に対して点$A$のある弧とは逆の弧上に$D^{‘}$を取ります。そうすると、円周角の定理より、円周角が中心角の半分の角度であることと、$\angle CAB$と$\angle CD^{‘}B$の二つの中心角の和が$360^{\circ}$であることを併せて考えれば、$\angle CAB+\angle CD^{‘}B=180^{\circ}$であることが分かります。

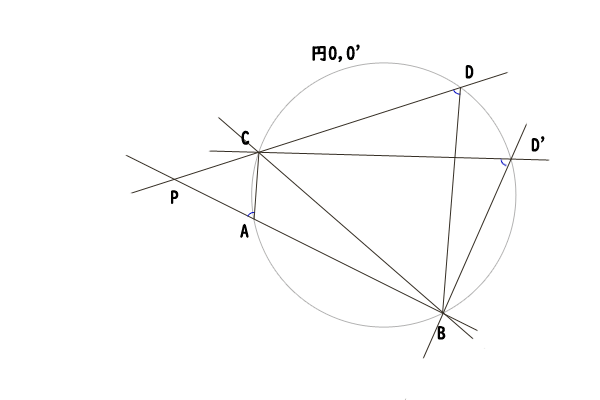
図１３：四角形が円に内接する条件の説明１

したがって、$\angle CD^{‘}B=180^{\circ} – \angle CAB$が成り立ちますが、$\angle PAC$は$\angle CAB$の外角なので、$180^{\circ} – \angle CAB=\angle PAC$となるので、$\angle CD^{‘}B=\angle PAC$が分かります。そうすると、いま$\angle PAC=\angle CDB$が命題の条件なので、$\angle CDB=\angle CD^{‘}B$が分かりました。

そうすると、点$D,D^{‘}$は直線$CB$の同じ側にあり、$\angle CDB=\angle CD^{‘}B$なので、やはり円周角の定理の逆より、点$C,D,D^{‘},B$はただ一つの円周上にあることが分かりました。三角形$CDB$に着目すれば三角形の外接円はただ一つなので、点$C,D,D^{‘},B$は円$O^{‘}$上にあることが分かりました。

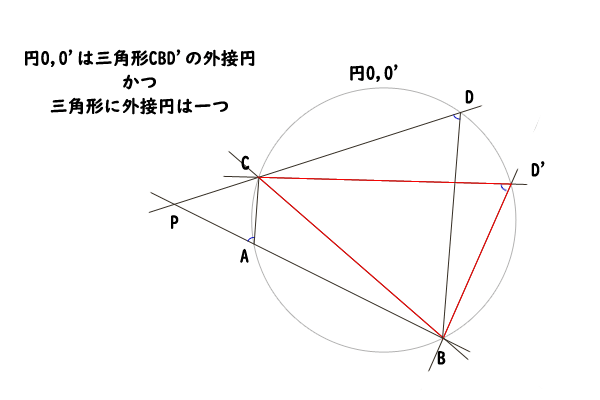
図１４：四角形が円に内接する条件の説明２

ここで、三角形$CD^{‘}B$に着目すれば、三角形$CD^{‘}B$は円$O$上、円$O^{‘}$上、共に存在することになりますが、三角形の外接円はただ一つなので、円$O$と円$O^{‘}$は同一の円であることが分かりました。そして、円$O,O^{‘}$はそれぞれ三角形$CAB$と三角形$CDB$の外接円なので、点$A,C,D,B$はただ一つの円周上にあることが分かります。

以上で、四角形の一つの内角が、その対角の外角に等しければ、四角形はただ一つの円周上にあることを示すことができました。
《四角形が円に内接する条件の証明終了》

②－Ⓐ：

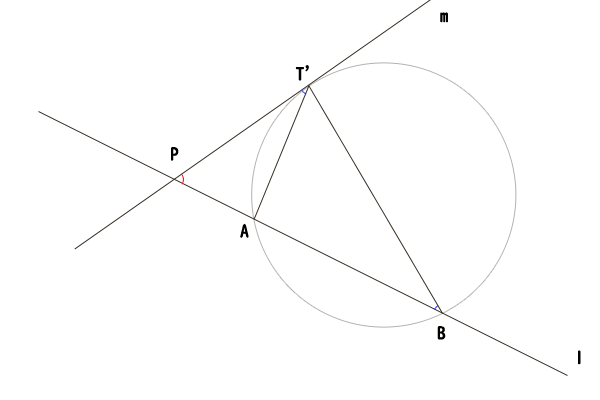
図１５：点$A,B$と点$C,D$が共に点$P$を挟んでいないで、点$C,D$が点$P$とは異なる同一点$C=D=T^{‘}$である場合

それでは、話を戻して、点$A,B$と点$C,D$が共に点$P$を挟んでいない場合で、点$C,D$が点$P$とは異なる同一点$C=D=T^{‘}$であるときの証明に入りたいと思います。点$A,B$が点$P$とは異なる同一点$A=B=T$であるときも、同様に証明することができます。

まず、三角形$APT^{‘}$と三角形$T^{‘}PB$について、共通の角なので$\angle APT^{‘} = \angle T^{‘}PB$が成り立ち、$PA\cdot PB = PT^{‘}\cdot PT^{‘}$より$PA:PT^{‘}=PT^{‘}:PB$が成り立つので、三角形$APT^{‘}$と三角形$T^{‘}PB$は相似であることが分かります。そうすると、$\angle PT^{‘}A = \angle PBT^{‘}$が成り立ちます。

仮に、点$ABT^{‘}$のただ一つの外接円が直線$m$と点$T^{‘}$で接しているならば、接弦定理（参照：接弦定理の証明、デカルトの探究方法を添えて）により、$\angle PT^{‘}A = \angle PBT^{‘}$が成り立つことになります。

ここでは、$\angle PT^{‘}A = \angle PBT^{‘}$ならば、点$A,B,T^{‘}$が直線$m$と点$T^{‘}$で接しているただ一つの円周上にあることを示したいわけですが、この結論部分は、何度も見てきた通り、三角形の外接円はただ一つに定まるので、点$ABT^{‘}$のただ一つの外接円が直線$m$と点$T^{‘}$で接していることと同値なります。したがって、上記の接弦定理の逆を証明することができれば良いということになります。

それでは、接弦定理の逆の証明を行いたいと思います。

《接弦定理の逆の証明開始》
証明の方法は、色々とあると思いますが、ここでは接弦定理の成立を前提とする最も簡潔な証明方法を紹介したいと思います。接弦定理を用いずに細々と場合分けをして証明をすれば必要な前提が明確となり、幾何学的なイメージも豊かに広がると思うのですが、本筋と離れてしまうのでそのような別解はここでは割愛いたします。

まず、異なる直線$l,m$を取ります。直線$l$上に左から点$A,B$を取り、直線$m$上に左から点$P,T^{‘}$を取り、$\angle PT^{‘}A = \angle ABT^{‘}$となることが、命題の仮定となります。この仮定から、三角形$ABT^{‘}$の外接円が直線$m$と点$T^{‘}$で接していることを示します。ちなみに、直線$m$上で点$P$が点$T^{‘}$の右側にあるときもすべてを対称にして、同様に考えれば証明ができます。

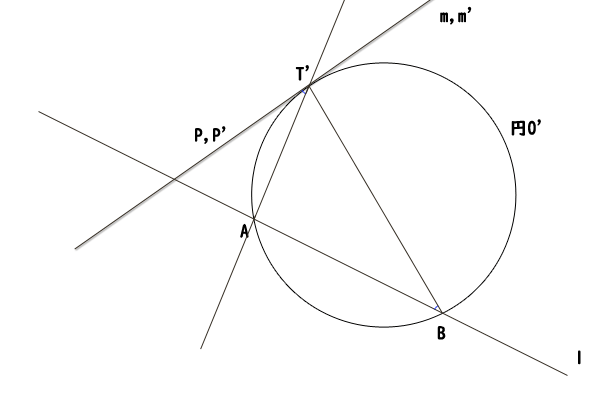
図１６：接弦定理の逆の証明

三角形$ABT^{‘}$のただ一つの外接円を円$O^{‘}$とします。点$T^{‘}$は円$O^{‘}$上の点なので、点$T^{‘}$を接点とする円$O^{‘}$に接する接線$m^{‘}$を引くことができます。次に、接線$m^{‘}$上の点$T^{‘}$の左側に一点$P^{‘}$を取ります。そうすると、接弦定理により、$\angle P^{‘}T^{‘}A = \angle ABT^{‘}$が分かります。

したがって、命題の仮定$\angle PT^{‘}A = \angle ABT^{‘}$と合わせて、$\angle PT^{‘}A = \angle P^{‘}T^{‘}A$が分かりました。直線$T^{‘}A$に注目すると、直線$m$と直線$m^{‘}$は、直線$T^{‘}A$上の一点$T^{‘}$を通り、直線$T^{‘}A$となす角が等しいことが分かります。したがって、直線$m$と直線$m^{‘}$が一致することが分かりました。

つまり、直線$m$は、三角形$ABT^{‘}$のただ一つの外接円$O^{‘}$の点$T^{‘}$を接点とする接線であることが示せました。
《接弦定理の逆の証明終了》

これで点$A,B$と点$C,D$が共に点$P$を挟んでいない場合で、点$C,D$が点$P$とは異なる同一点$C=D=T^{‘}$であるときの証明が済みました。

②－Ⓑ：

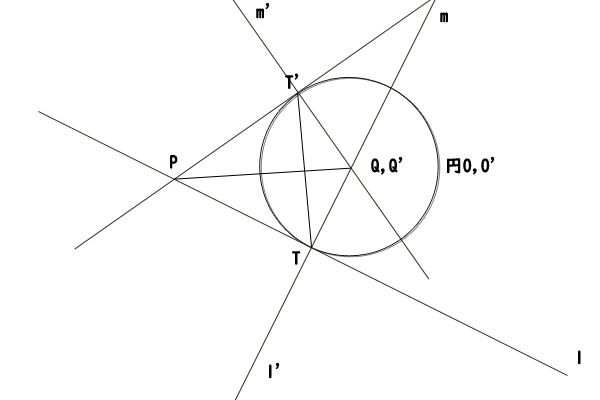
図１７：点$A,B$と点$C,D$が共に点$P$を挟んでいないで、点$A,B$と点$C,D$が共に同一点$T,T^{‘}$である場合

次は、最後に、点$A,B$と点$C,D$が共に点$P$を挟んでいない場合で、点$A,B$と点$C,D$が共に同一点$T,T^{‘}$である場合には、点$T$と$T^{‘}$が接点となるただ一つの円があることを証明します。

直線$l$に点$T$を足とする垂線$l^{‘}$、直線$m$に点$T^{‘}$を足とする垂線$m^{‘}$を引きます。そこで仮に、直線$l^{‘}$と直線$m^{‘}$が一致する又は平行であるとすると、その同位角が等しいので直線$l$と直線$m$も一致するか又は平行となり、直線$l$と直線$m$が点$P$において交わることに矛盾します。したがって、直線$l^{‘}$と直線$m^{‘}$は一致せず、かつ、平行でもないので、一つの交点を持ちます。その交点を点$Q$としましょう。

三角形$QPT$と三角形$QPT^{‘}$について、辺$PQ$は共通であり、$PT^{2}={PT^{‘}}^{2}$より$PT=PT^{‘}$であり、$\angle QTP= \angle QT^{‘}P=90^{\circ}$であり、直角三角形の２辺が等しいので、三角形$QPT$と三角形$QPT^{‘}$は合同であることが分かります。したがって、$QT=QT^{‘}$であり、点$Q$を中心として半径$QT$の円を円$O$とすると、円$O$上に点$T,T^{‘}$があることが分かります。

円$O$の中心を通る直線$l^{‘}$が円$O$上の点$T$において直線$l$と垂直に交わっているので、直線$l$は円$O$の点$T$における接線であることが分かります（参照：円と直線の距離と位置関係、特に交点、接点、接線について：このページの最終目標：【命題２】）。同様に、直線$m$は円$O$の点$T^{‘}$における接線であることが分かります。

次に、仮に、点$T$と点$T^{‘}$が接点となる円$O$とは異なる円$O^{‘}$があったとして、その中心点を$Q^{‘}$とすると、円$O^{‘}$は点$T$で直線$l$と接するので、直線$l$と直線$TQ^{‘}$は直交します（参照：円と直線の距離と位置関係、特に交点、接点、接線について：このページの最終目標：【命題１】）。したがって、直線$l^{‘}$と直線$TQ^{‘}$は、共に直線$l$と点$T$で直交するので、直線として一致します。つまり、点$Q^{‘}$は直線$l^{‘}$上にあることが分かりました。同様に、点$Q^{‘}$は直線$m^{‘}$上にあることも分かります。直線$l^{‘}$と直線$m^{‘}$の交点はただ一つ点$Q$しかないので、点$Q$と点$Q^{‘}$が一致することが分かりました。

さらに、$TQ=TQ^{‘}$で半径も等しいので、円$O$と円$O^{‘}$は一致することになりますが、これは仮定と矛盾します。したがって、円$O$は点$T$と点$T^{‘}$が接点となるただ一つの円であることが分かりました。

以上で、命題のすべての場合を証明することができました。□

最後に、このページの【方べきの定理】では、円$O$上に点$P$がない場合に限定しましたが、$P=A$又は$P=T$の場合に、$PA=0$又は$PT=0$とみなせば、円$O$上に点$P$がある場合を含めて【方べきの定理】が成立します。すなわち、円$O$上に点$P$がある場合には、方べきは$0$となり、一定であるからです。

そうすると、【方べきの定理】は平面上のすべての点において成立することになります。さらに、次の疑問としては、方べきの値が点$P$の位置によってどのように変化するのかも気になるところです。その他にも色々な疑問が湧きますが、課題としては自由研究として調査してみるのに丁度良い難易度かもしれません。面白い内容を見つけることができましたら、ご連絡いただければ幸いです（連絡先は、弊社HPに記載しております）。

著者：L&M個別オンライン教室　瀬端隼也
公開日：２０２０年３月１０日
修正日：ー