図形と方程式とデカルト、高校数学と科学の基礎について

【目次】
０．はじめに
 １．デカルト以前の科学の状況
　　１―１．幾何学について
　　１―２．代数学について
　　１―３．微分、積分について
 ２．デカルトが方法序説で主張したこと
　　２―１．幾何学の論理体系
　　２―２．対象と関係
　　２―３．関係を数の組、線、文字で表す
　　２―４．科学の一般理論
　　２―５．幾何と代数の相互補完
 ３．図形（点）と方程式（数の組）の一致と包含関係による証明
 ４．デカルト以後の科学、影響と位置付け
　　４―１．ニュートン力学、微分と積分の結合、科学一般
　　４―２．異なる流れと互いの位置付け
 ５．まとめ

はじめに

このページでは、高校数学の教科書（詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください。以下同じ。）の数学Ⅱ第３章「図形と方程式」が高校数学ひいては現代科学の基礎中の基礎になっていることを高校生でも分かるように解説したいと思います。

この章の冒頭コラムにデカルトが紹介されている通り、その主人公はデカルトです。デカルトが革新した科学の流れを知ることで、高校数学を体系的に理解することができ、科学の諸分野の土台となる高校数学の学力を深く効率的に育むことができます。

例えば、高校数学を学び始めたとき、数と式や２次方程式は抽象的で難しいと感じたことはありませんでしょうか。それは、デカルト以前のすべての数学者が感じていた難しさと同じ困難を味わっている、と考えれば当然のことです。

上記コラムでも触れられていますが、デカルトが座標つまりグラフを発見したのですが、その発見によって数と式や２次方程式への理解は飛躍的に進み、また理解しやすいものになりました。そのため、数学Ⅰの教科書でも２次方程式と２次関数はほとんど同時に学習するように配置されています。

したがって、数学の体系からすると、初めはたしかに数と式や２次方程式を単独で学ぶ必要がありますが、ある程度理解が進んできたら速やかに座標の理解を深めて、それまで学んできた幾何学と結びつけながら学習を進めることが効率的であり、理解を深める学習のコツとなるわけです。

このように、以下、本ページでは、より詳細に高校数学つまりは科学の基礎を体系的に理解するために有用な内容を解説していきたいと思います。

デカルト以前の科学の状況

幾何学について

デカルトやガリレオ以前の科学は、科学という言葉も現在の意味とは異なり、天動説が一般的で運動の法則もあいまいなものでした。ただ、幾何学はユークリッドの原論が古代ギリシャ文明の集大成として存在しており、現在、中学や高校で学ぶような論証を用いた平面図形や立体図形についての高度な知識はすでにありました。

一方で、「天動説が一般的で運動の法則もあいまい」という状況から何とか想像できるかもしれませんが、平面や空間内の図形を現在のように座標を用いて方程式や数の組で表す方法は発見されていませんでした。現在では、小学生や中学生でも理解できそうな簡単なことのように感じるかもしれませんが、座標やグラフも、当たり前の概念のように思える数や図形、論理などと同様に、人によって発見されてきたものなのです。

代数学について

代数学は、アラビアの数学者アル・フワーリズミーが発見したものが西洋に流入したと言われています。ただ、その頃の記法は現在のように簡略化されて整ったものではなかったようですし、幾何学との対応も数学者を悩ませる難題となっていました。

例えば、冒頭コラムにも紹介されていますが、\(x^2\)は長さ×長さだから面積だという現在からすれば幾何学に偏重したたんなる偏見によって、\(x^2+x\)は面積＋長さを意味するおかしな数式だと考えられていました。面積なのか長さなのか、どんな量として解釈すべきか分からないということです。結局のところ、デカルトがその偏見を拭い、\(x^2\)も長さを表す量として考えれば不都合はない点を指摘し偏見は克服されました。

あるいは、\(y=x+1\)のような２変数の数式も解が決まらないので解釈が難しかったようです。これもデカルトが平面内の軌跡を提示することで線を表すことを明示し、立派な意味のある数式として認識されるに至りました。おそらくある数式の解釈が定まらない、理解しにくいということは、高校数学でも割と多く直面する困難の一種類ではないかと思います。したがって、この過去の経緯から私たちが学べることは、その多くは、あくまでもすべてではありませんが、デカルトが発見した座標を対応させることで解決するだろうと思います。

微分、積分について

曲線の接線の傾きの計算法としての微分、面積や体積の計算法としての積分は、極限を用いた計算法として古代ギリシャより研究されていたようですが、その各々は独立したもので互いに関係し合うという認識はありませんでした。

もちろん、座標はありませんでしたので、上記はあくまで幾何学における平面図形や立体図形の量の具体的な計算にとどまっていたことも大切なポイントです。つまり、現在のように方程式、関数での微分、積分の表現はできていなかったということです。くわえて、詳しくは後述しますが、現在のように例えば速度や力、エネルギーのように幾何学以外の対象の微分、積分についてはそのほとんどは霧の中にありました。

これらはすべてデカルト以後に、デカルトが発見した座標によって、つまりは文字通り「デカルトが準備した科学理論」の中で発展していくことになります。

デカルトが方法序説で主張したこと

デカルトは、座標の発見を論文で報告するだけではなく、その序文的な著書『方法序説（本ページでは岩波文庫を用います。以下同じ。）』で座標発見に至る過程、その探究方法から何を意図して発見に至ったかまでを詳述してくれています。ここでは、デカルトが方法序説で主張した指摘の中でも特に座標に関連する内容を取り上げて確認したいと思います。

幾何学の論理体系

デカルトのような偉大な学者ともなると当然のこととして、何を発見したのかだけではなく、どうすれば発見ができるのかその探究方法から考察します。その方法としてデカルトが紹介したのは２ページにも満たない４つの規則と説明です。ここでは座標との関係が薄れるのでその詳しい解説は避けますが、その方法は幾何学の論証を参考にして洗練されたものです。彼の時代の幾何学というのは、先述したユークリッドの原論を中心とする古代ギリシャ文明で集大成されたものです。

『自分が疑問を差しはさむ余地のまったくないもののみを真としてと認め、複雑な問題は適切に分割し、単純なものから複雑なものへ順序を付けて、真のものから真のものへと推論、演繹を続ける、最後に完全な枚挙と全体の見直しをすること』、これが彼が幾何学の中に見た論理学のエッセンスとして抽出した探究方法の概略です。

そして、彼がこの探究方法をまず一番に用いてみたのが数学や科学の分野であり、そこで現在の座標概念を含む幾何学と代数学を融合した学問を発見したと続けて述べていきます。

対象と関係

数学や科学を上記方法で探究していく中で、デカルトは適切に分割された最も単純なものとして、次の発見をしたのでしょう。つまり、まず初めにこう述べています、分かりやすいように抜粋すると、

「これらの学科が、対象は異なっても、そこに見いだされるさまざまな関係を考察する点で一致する」

対象というのは、何かを考えているときのその「何か」のことで、関係というのはその対象の間で両者に関わる、やはり、「何か」のことです。一般的な用語と同じ意味と考えて問題ありませんが、例えば、人間関係という言葉であれば、対象である人の間の関係という意味になります。

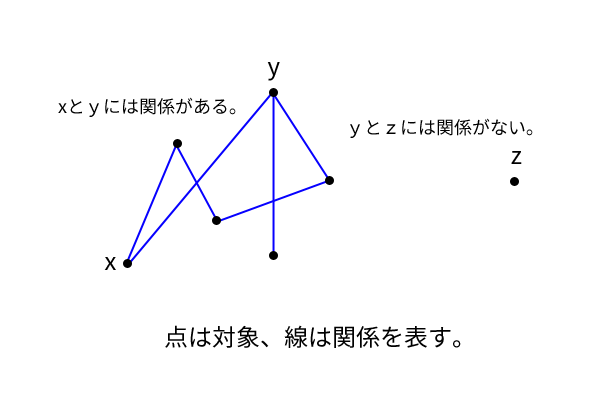
図１：対象と関係

さらにデカルトは、進めてこの関係（後述しますが、デカルトの場合は比例）だけを一般的に検討するのが良いと見定めます。つまり、デカルトがここで主張することは、数学や科学は、異なる学科でそれぞれ異なる対象を扱っているが、結局、主に考察しているのは対象ではなく、そこに見いだされるさまざまな関係の方だと言うわけです。人間関係で言えば、その人よりもその人を取り巻く人間関係を考えようというのです。

哲学的な基礎としての詳しい解説は、座標の話から離れてしまうので避けますが、デカルト以後の偉大な数学者や科学者（アインシュタイン、ヒルベルトなど）は概ねこの意見に同意しているのはたしかです。つまり、科学は対象間の関係を調べる学問であるということです。

この指摘は、後ほどデカルト以後の科学に触れる際に再び取り上げたいと思いますが、数学や科学を学んでいくうえで、それらに出てくる内容を整理して論理的に考察するためには基本的な認識であり、とても役に立つ枠組みとなります。つまり、何を学んでいるのかを意識し、それらの関係を整理していくのです。

一言で、なぜ？という疑問に答えると、関係のないことを考えても仕方ないし、関係を知るほど対象を知ることになるから、と言えばよいでしょうか（疑問を感じる方はこの枠組みを超える探究もぜひ将来おこなってください）。とにかく、デカルトはさらに具体的に数学や科学ではどのような関係をどのように取り扱えばよいのかという考えに進んでいきます。

関係を数の組、線、文字で表す

結論から言うと、デカルトはこの関係として「比例だけを考察する点で一致する」と見定め、「比例だけを一般的に検討する」方針を取りました。比例とは、狭義には\(y=ax\)のように一定の割合で変化する二つの数の組のことを意味しますが、より広い意味としては二つの数の組の比や割合の変化、あるいは、一般論としてはただの二つの数の組の変化のことを指していると考えて良いと思います。

さらにデカルトは、その比例を「私にいっそう容易に認識させてくれるのに役立つような対象」を探し、「これを線として想定すべき」、なぜなら「線以上に単純で、線以上に判明にわたしの想像力や感覚に表象できるものはなかったからだ」とします。つまり、比例や数の組の関係を幾何学における線で表そうとし、座標やグラフの発想が形作られていきます。ちなみに、デカルト以前は今日の座標のように二つの数の組の変化を線（や点）で表そうとする発想すらなかったことを忘れてはいけません。ただ、同時期に独立してフェルマーも思い付いていたそうです。

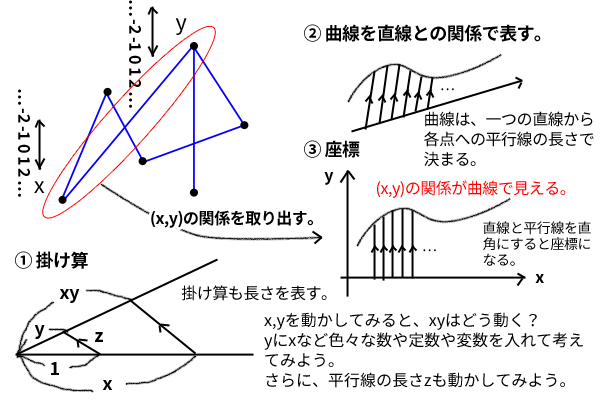
図２：比例関係を数の組、線、文字で表す
（参考文献：幾何学、ちくま学芸文庫）

さらにデカルトは、「それらの比例を記憶に保持し、多くを一度に捉えるためには、できるだけ短い、ある種の記号で示す必要があること」として、比例を表す幾何学上の線を代数式で表す方法を発見し、座標の発見へとつながって行きました。その際のポイントとしては、前述のデカルト以前の「代数学について」でも触れましたが\(x^2\)を面積として解釈するなどの偏見を拭い、代数の積も単なる長さとして線として解釈できるというデカルトの「自分の頭で考える」探究方法の成果が大きな役割を果たしています。

具体的には、デカルトは比例を線として表わすとしましたが、比例を個別的に考察するには二つの数の組を点として捉える必要があり、その際に座標の位置は各座標軸の長さで表されなければなりません。つまり、\(y=x^2\)を座標上の線として表わすには、\(x^2\)を\(y\)軸上の線、そして長さを表す数として偏見なく認識する必要があったわけです。

このようにして数学や科学で表れるさまざまな関係を時には個別的に時には多くを同時に座標の上の線として、数の組（比例）として、代数として、捉えることができるようになりました。つまり、デカルトが\(x\)というときは\(x\)軸上の線の名前であり、線の長さを表す数でもあるということで、デカルトが\(y=ax\)というときは２次元座標上の直線の名前であり、比例（数の組）でもあるということです。

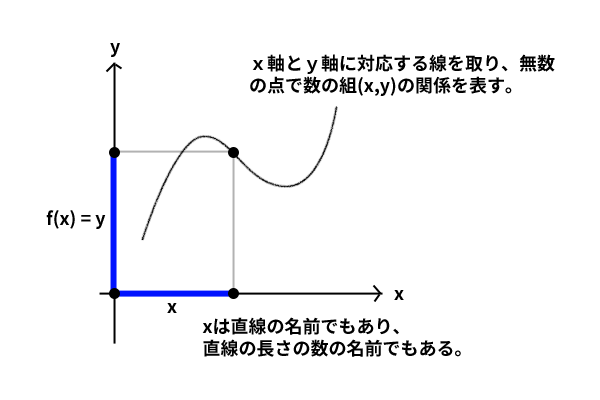
図３：数の組、線、文字の対応

ここに文字通り、記号（代数式）、数、線の結合が果たされ、幾何学と代数学が融合されました。数学や科学で表れるさまざまな「見えない」関係、つまり数の組の関係を「見える」座標の上の線として表わすことができた画期的な瞬間だったと言えます。このことは次の節でさらに詳しく解説しますが、これこそデカルトの意図通りの発見であったとも言えるのです。

ちなみに、現在でも数式の定数を表す時にはアルファベットの前半\(a, b, c, …\)を用い、変数を表す時にはアルファベットの後半\(… x, y, z\)を用いますが、このような使い分けや「できるだけ短い」単純な記号を用いる形式もデカルトから始まったと言われています。

科学の一般理論

ここまでデカルトは、数学や科学は異なる対象であっても、さまざまな関係だけを考察している、さまざまな関係であっても比例（数の組）だけを考察していると考えを進め、これを抽象と言いますが、さらに比例（数の組）を線で表し、これを記号（代数式）で示すとして座標を発見しました。その際に、このように考えを進める意図を次のように述べています。

「これらの比例だけを一般的に検討するのがよい、その際そうした比例を、わたしにいっそう容易に認識させてくれるのに役立つような対象があれば、そのなかにだけ想定し、しかもそうした対象にだけ限るのではなく、それが当てはまるような他のすべての対象にも、後になっていっそううまく適用できるようにする」

上記引用文を解説すると、「いっそう容易に認識させてくれるのに役立つような対象」とは、比例（数の組）を容易に表すその対象として、結局、線と記号（代数式）つまり座標をデカルトは見つけることができました。「それが当てはまるような他のすべての対象」とは、数学や科学の異なる対象とその間のさまざまな関係ということになります。

つまり、デカルトは数学や科学の異なる対象から関係、そして比例を取り出し、より認識しやすい線と記号の座標などの形で表し、いったんそこで考察した結果を後から数学や科学の異なる対象と関係に適用し直す、という構想を初めから目標としたうえで座標などを発見したということになります。

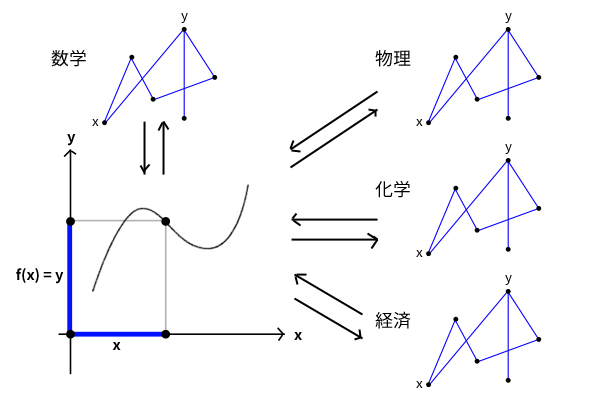
図４：　科学の一般理論としての座標

そして、実際に歴史がその大胆な試みが成功したことを示してきました。つまり、座標を学び始めたばかりの方は、おそらく座標は平面や空間を表すためだけのものと思いがちですが、デカルトの意図通り、座標は幾何学とは何の関係もないように思える他の科学の諸分野（例えば、エネルギー変化、化学反応、細胞増殖、貨幣価値など、位置以外の色々な変数を取れるということです）についても、その目には見えない数の組の法則を数式で表し、座標で表し、目に見える図形に表すことができてしまうのです。

さらには、座標などの上に表れた図形に幾何学の法則を適用して何らかの発見があれば、あるいは、微分積分学のような代数と幾何の融合である座標上で発展した数学上の理論も、デカルトの意図通り「後から数学や科学の異なる対象と関係に適用し直す」ことができるのです。

これは当時の人々からすると想像すらできない、深遠な理論になっているわけです。しかし、歴史はすぐに座標上で表される目には見えないはずのニュートンの力学、微分積分学へとつながります。そして、当初のデカルトの意図通り、座標は科学の一般理論として、もちろん数学を含めて大いに役立ってきたのです。

デカルトを知らず方法序説を読んだことがないときには、座標は平面や空間を表すために自然発生的に発見され、それが他のさまざまな科学的な量を表すことにも使われるようになったのではないかと誤解してしまうかもしれませんが、それはここまで見てきたように逆で、そもそもデカルトは初めから科学一般に用いることができる理論を模索して座標を見つけたわけです。驚くべきことですが、ここがデカルトの凄味であって、湯川博士がその著書「創造への飛躍」でデカルトを天才の中の天才と評したゆえんであると思います。

ちなみに、この科学の一般理論としての座標の性質、つまり、座標の数の組、線、代数は扱う対象に縛られていないという性質、あるいは、各座標として色々な変数を取ることができるという性質を理解することは、高校数学で微分積分学を学ぶ際にも大いに役立ちます。そもそも、\(x^2\)が面積を表すのではなく長さを表すと解釈してもよいというデカルトによる偏見の排除が重要な出発点でしたが、これを一歩進めると、それは数をその対象から切り離し単純に数とみることができるという考え方であり、この考え方は微分積分学を学ぶ際に初学者が陥りがちな次のような偏見にも適用できるのです。

つまり、微分積分学の学び初めにはおおむね、傾き、長さ、面積、体積という幾何学的な対象の量と数を分かち難いものと考えてしまい、例えば、体積を考えるには必ず３次元を考えなければいけない、というような偏見を拭い切れないでいます。しかし、これらの幾何学的な対象の量もその対象から切り離せば単純な数であり、座標の「各座標として色々な変数を取ることができるという性質」に改めて当てはめられるのです。

例えば、体積を表す１変数関数が分かるのであれば、それを数式にすれば２変数であり、２次元座標つまり平面座標の曲線として体積を表すことができます。そして、それを微分した平面座標上で傾きとして表わされた数は、元々の体積の微分係数、つまり、体積の切り口の面積を表すように設定することもできます。あるいは、面積を表す１変数関数が分かるのであれば、それを数式にすればやはり２変数であり、２次元座標つまり平面座標の曲線として面積を表すことができます。そして、それを積分した平面座標上で面積として表わされた数は、元々の面積の積分、つまり、体積を表すように設定することもできます。

このように平面座標上の曲線に置き直してしまうという考え方は、特に一般的な関数の微分積分を考え始めるときには有用です。それは、元々デカルトがさまざまな関係を比例（数の組）のみで、そしてそれを線（曲線）で表すといったように平面座標内の曲線はとても認識しやすい対象だからです。偉大な先人の思考は、過去のものではなく、現在の私たちに対しても常に多くの示唆を与えてくれるものです。

幾何と代数の相互補完

そしてデカルトは、方法序説での数学理論についての導入を次のような言葉で締めくくります。

「このようなやり方で、幾何学的解析と代数学とのあらゆる長所を借り、しかも一方の短所すべてをもう一方によって正せる」

幾何学の長所は、目に見える具体性を備えていること、短所は、その具体性のために偏見が生まれ他の数学や科学と上手く関係付けることができなかったことです。代数学の長所は、目に見えない抽象性を備え他の数学や科学を扱いやすいこと、短所は、その抽象性のために直観的な考察が難しかったことです。

デカルトは、この両者の長所と短所を互いに補い合えると主張したわけです。実際に、前節でも触れたように抽象的な代数式は座標上の線として表わされ、これにより例えば、方程式の実解と虚解の違いは\(x\)軸との交点の有無として具体的に理解できるようになりました。一方で、幾何学の複雑な曲線は代数式として表わされ、これにより例えば、２曲線の交点は２つの方程式の共通解を得ることで正確に位置を突き止めることができるようになりました。その上、微分積分学などは代数学にとっても幾何学にとっても新たな理論の展開であったと言えます。

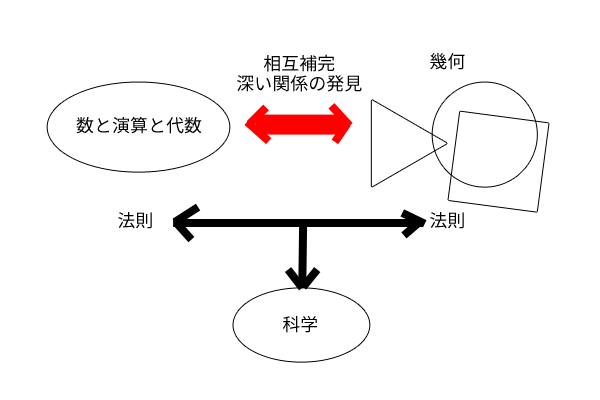
図５：代数と幾何の相互補完

まさにデカルトの主張通り、当時の人々からすると異なる分野と思われていた幾何学と代数学の深いつながりを発見することで、一方で培われた法則や考察がもう一方へと流れ込み、相互に発展を促し、互いに一致して発展していくことになりました。

この歴史的な展開は、現在の私たちが高校数学を学ぶうえでも、ひいては数学や科学を学んで行くうえでも大きな示唆を与えてくれます。つまり、高校数学の教科書を学ぶ際には、各単元で代数に関すること、幾何に関することを初めは別々に学ぶしかないですが、一通り学んだ後には、両者を座標上で繋げて互いの関係を意識しながら学ぶ方が効率も良く理解も深くなるということです。同様に、他の数学や科学を学ぶ際にも、座標の科学の一般理論としての性質を理解し、一度、座標上に考察を移し座標上で培った知見を活かしきるというアプローチを模索してみて、それができればやはり効率も良く理解も深くなる可能性が高いということです。

さらに、一歩考えを進めれば座標に限らず、デカルトが幾何学と代数学をつなげたように、ある一分野の中だけで考えていても煮詰まってしまった物事でも他の分野とのつながりを発見することでそれらの分野の理解を深めることができます。この事実を活用すれば、つまり、一分野に閉じこもらず他の分野との関係を視野に入れながら学習することで学習効率も理解深度もさらに一段と高まっていきます。

図形（点）と方程式（数の組）の一致と包含関係による証明

座標上で図形を方程式によって表すためには、描きたい図形を方程式が本当に描いているのかを証明する必要があります。正確に言うと、描きたい図形を表す無数の点と方程式の解となる数の組が表す無数の点とが一致していることを証明する必要があり、その論法は図形が単純であろうが複雑であろうがどんな図形であっても同じです。

そこでここでは、円についてその証明方法を例示したいと思います。この論法をしっかりと理解すれば図形と方程式の範囲の理解が一段と深まります。一度きちんと理解すれば必ずしもいつも考察を繰り返す必要はなくなります。

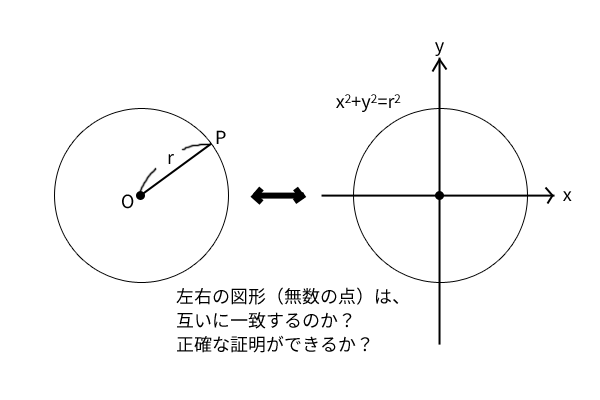
図６：図形（点）と方程式（数の組）の一致

まず、ある点\(O\)を中心として半径\(r\)の円を描きたいとします。円周上のどの点であっても良いので点\(P\)と名付けます。そうすると、この各点\(O, P\)と半径\(r\)は\(OP=r\)という関係式を満たすことが分かります。そして逆にこの関係を各点\(O, P\)が満たせば点\(P\)は円周上にあり、満たさなければ点\(P\)は円周上にないことが分かります。なぜなら、\(OP\neq r\)を満たす点\(P\)は半径\(r\)ではない円周上にあるからです。

仮に、描きたい図形である点\(O\)を中心とした半径\(r\)の円（無数の点）と関係式\(OP=r\)を満たす点\(P\)が描く図形（無数の点）が一致しないとすると、少なくとも一点について、前者か後者かいずれかに入り、かつ、もう一方に入らないはずです。これは前者に入れば後者に入り、後者に入れば前者に入るという前段の包含関係に関する主張と矛盾します。したがって、描きたい図形である円と関係式\(OP=r\)を満たす点\(P\)が描く図形は一致することが分かります。

ここまでは、座標や数の組が出てきていないことを意識してください。次に、点\(O\)を中心に\(x\)軸と\(y\)軸を描きます。これによって\((x,y)\)で表される無数の数の組と平面上の無数の点が対応関係を持ちます。そこで改めて点\(P\)を表す座標を変数として\((x,y)\)と置きましょう。このとき\((x,y)\)は動く数の組でありつつ、同時に\(x\)軸と\(y\)軸上に表れる線の名前でもあると認識してください。

そうすると、先ほどの描きたい図形である円の関係式\(OP=r\)を満たすいずれの点も、幾何学のピタゴラスの定理により、幾何学的に方程式\(x^2+y^2=r^2\)を満たすことが分かり、同時に、数の組として方程式\(x^2+y^2=r^2\)の無数の解に含まれることが分かります。一方で、方程式\(x^2+y^2=r^2\)を満たすいずれの解も、座標の\(x\)軸\(y\)軸との対応を付けると、やはり幾何学のピタゴラスの定理により、幾何学的に描きたい図形である円の関係式\(OP=r\)の無数の点に含まれることが分かります。

仮に、描きたい図形である円の無数の点と方程式\(x^2+y^2=r^2\)が座標上で表す無数の点とが一致しないと仮定すると、少なくとも一点は前者か後者かいずれかに入り、かつ、もう一方に入らないはずです。これは前者に入れば後者に入り、後者に入れば前者に入るという前段の包含関係に関する主張と矛盾します。したがって、描きたい図形である円の無数の点と方程式\(x^2+y^2=r^2\)が座標上で表す無数の点とが一致することが証明できました。

つまり、描きたい図形である円を方程式\(x^2+y^2=r^2\)が本当に描いていることを証明できました。

デカルト以後の科学、影響と位置付け

ニュートン力学、微分と積分の結合、科学一般

すでに触れたかと思いますが、デカルトが座標概念を発見した後に、その基礎の上にニュートンが彼の力学と微分積分学を確立しました。座標によって空間を表すという思想無くして、物体の運動を数式で表すというその出発点もなかったわけです。

微分積分学も冒頭で別々に独立して接線の傾きを求めたり、面積や体積の求積法はあった旨を述べましたが、それらが逆演算であること、つまり、ある関数\(y=f(x)\)を微分したものを積分した関数、あるいは、積分したものを微分した関数が元の関数\(y=f(x)\)に戻ることは知られていませんでした。

このことを微分積分学の基本定理とも呼びますが、この定理も座標概念による見通しのよさがその発見へとつながったことは明らかです。この定理により、微分によって解明された公式が積分へ、積分によって解明された公式が微分へと、互いに生かすことが可能になり、デカルトが代数と幾何をつなげたときのように、相互補完的に発展が加速しました。例えば、置換積分や部分積分の公式などですが、この理論の肝、全体像を知っておくことも個別の知識を理解し、使いこなすためにきっと役に立つことと思います。

さらに、ニュートンが微分積分学を駆使して示してくれた彼の力学においては、エネルギー保存則など目には見えない奥深い自然法則を簡潔な数式と座標上の表現で私たちに直観的にも理解しやすいものとして示してくれました。私たちが今、明らかだと信じている事象は、当時の人々には決して明らかではない不思議な理論であったことを忘れてはいけないと思います。

異なる流れと互いの位置付け

デカルトの発見した座標は、数学と科学の歴史においてかなり大きな主流を占めていると言っても過言ではありません。しかし、どんな分野の学問も多かれ少なかれ互いに関係し合って発展していくものですが、デカルトの思想とは異なる源流をもっているだろう数学や科学の分野ももちろんあります。ただ、冒頭でも少し触れていますが、デカルトは学問全般をかなり一般的な視点から考察し、根本的な基礎にも指摘を残した学者ですので、それらの異なる源流の理論もどこかしらデカルトの指摘の一部に位置付けられないこともありません。

例えば、同時代のパスカルやフェルマーが創始したと言われる確率論は、場合の数や組合せを源流としていますが、これらは少なくとも科学は対象間の関係を扱うというデカルトの指摘に含まれているでしょう。ガロアたちが方程式の解の公式についての研究から創始したと言われる群論等も同様です。目には見えない対象間の関係を人が認識する難しさがこれらの理論の発見を遅れさせたのだと私は感じています。

カントールが創始した集合論は、デカルトの数学や科学の基礎は論理学、形而上学にあるという態度に明らかに合致しています。集合論から明らかになった集合間の関係、写像等の本質性を源流として生まれ出たアイレンベルグとマックレーンが創始した圏論も、やはり科学は対象間の関係を扱うというデカルトの指摘から外れてはいません。

それどころか、デカルトの思想とは異なる源流をもっているだろう数学や科学の分野であっても、どれもデカルトが「関係を比例とする」、と言明した箇所を、「関係を〇〇とする」、と比例を別の関係に置き換えているに過ぎないようにすら見えるわけです。この点は、哲学者デカルトの卓越した点であると感じます。

まとめ

以上の高校数学や科学の知識は、理解することによってほぼ確実に社会の役に立つ知識と言えます。このような流れを知って体系化された知識を学ぶことによって、高校数学や科学を見通し良く学んでいくことができて理解も深まることと思います。逆に、このような流れを無視して個別分野の演習の反復やテスト勉強のためだけのマニュアル化を追及しても、それはそれで価値はありますが、それ以上に自分の頭でじっくりと学んだことは、どのような応用にも対応できる考える力となって次の分野への足取りを軽くしてくれるだろうと思います。

公開日：２０２２年１２月０７日
修正日：－

図形と方程式