恒等式の次数と係数、根の個数の条件の証明

【目次】
０．はじめに
１．恒等式の定義
２．一変数の恒等式の次数と係数の必要十分条件
　　２－１．一変数の恒等式の次数と係数の必要十分条件の解説
　　２－２．一変数の恒等式の次数と係数の必要十分条件の証明
３．$ｎ$次以下一変数の恒等式の根の個数の十分条件
　　３－１．$ｎ$次以下一変数の恒等式の根の個数の十分条件の証明
４．一変数の恒等式の次数と係数の必要十分条件の別証
　　４－１．発散する性質を使って
　　４－２．連続性を使って
　　４－３．微分可能性を使って
５．発展：線形代数や代数学の基本定理との関連

はじめに

このページでは、恒等式の定義の確認から始めて、高校数学の教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）の数学Ⅱ単元「式と証明」の節「式と計算」で「恒等式の性質」として証明なしで紹介されている一変数の恒等式の次数と係数の必要十分条件についての命題と、やはり証明なしで紹介されている$n$次以下の一変数の等式が恒等式となるための十分条件は$n+1$個の異なる根（解）を持つことであるという命題、この二つの命題を証明します。

それでは、まず恒等式の定義から確認しましょう。

恒等式の定義

高校数学の教科書によると、恒等式は次のように定義されています。

「等式に含まれている各文字にどのような値を代入しても、両辺の値が存在する限り常に成り立つ等式を、それらの文字についての恒等式という。」

「それらの文字について」とありますので、この教科書の定義によると、等式は一変数とは限らず一変数でも多変数でも良いことになります。ただ、教科書の本文で扱う内容や、このページで紹介する二つの命題は一変数の恒等式に関する内容に限定されます。ちなみに、教科書の番外編の【研究】では二変数の恒等式について取り扱っています。

また、「両辺の値が存在する限り」とありますので、「左右の辺どちらかの値が存在しない」ときには「等式が成り立たない」場合があっても恒等式と言えることになります。くわえて、やはり「それらの文字についての恒等式」とありますので、「それ以外の文字については」恒等式であるとは限らないことになります。したがって、恒等式といってもどの文字についての恒等式なのかを明確に理解することがポイントになります。

さらに、恒等式と方程式の違いや、数式とは何か、どう理解し扱えばよいかについては数式はなぜ文字を使うのか？をご覧ください。

一変数の恒等式の次数と係数の必要十分条件

【一変数の恒等式の次数と係数の必要十分条件】は高校数学の教科書では、以下のように紹介されています。

【恒等式の性質】
$P,Q$を$x$についての整式とする。

１．$P=Q$が恒等式　$\Leftrightarrow$　$P,Q$の次数は等しく、両辺の同じ次数の項の係数は、それぞれ等しい。

２．$P=0$が恒等式　$\Leftrightarrow$　$P$の各項の係数はすべて$0$である。

ちなみに、整式の定義については整式の割り算と余りの一意性、整数との比較や一般化について：定義と解説をご覧ください。

一変数の恒等式の次数と係数の必要十分条件の解説

まず、$P,Q$は$x$についての整式なので、仮に次数が$n$であれば、

$$a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0$$

のように$x$のべき乗とその係数$a$の積を項とし、その各項の和で書けることを押さえておきましょう。その上で、命題は前提としては次数を指定していないことに注意してください。にもかかわらず、命題１において「$P,Q$の次数は等しく」なると言明しているわけです。したがって、命題１の左から右を証明するには、「$P,Q$の次数は等しく」なることから証明を始める必要があります。

次に、整式$P,Q$をそれぞれ、

$$P = a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0 = f(x)$$
$$Q = b_mx^m+b_{m-1}x^{m-1}+\ \cdots\ +b_1x^1+b_0 = g(x)$$

とおけば、二次直交座標$xy$平面上のグラフとして、$y=f(x)$と$y=g(x)$を考えることができます。その上で、$P=Q$が恒等式になるという条件を解釈すると、どのような$x$についても$P=Q$が成り立つということは、どのような$x$座標についても$y$座標が等しくなるということなので、グラフ$y=f(x)$とグラフ$y=g(x)$が一致することと$P=Q$が恒等式になることが同値であることが分かります。

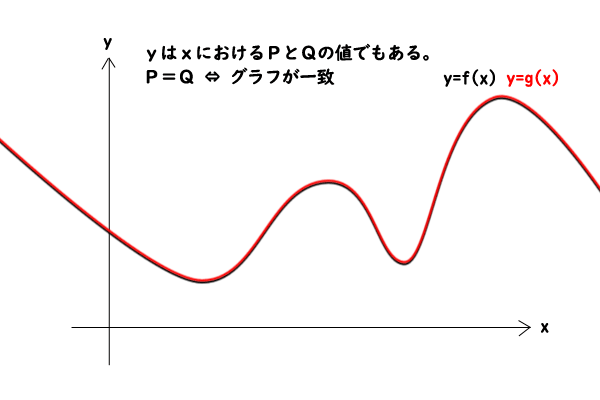
図１：恒等式とグラフの関係

そうすると、このグラフによる直観的な解釈によれば、命題１は整式（方程式）のグラフが一致すれば、その整式（方程式）の次数は等しく、両辺の同じ次数の項の係数は、それぞれ等しい。逆に、整式（方程式）の次数が等しく、両辺の同じ次数の項の係数が、それぞれ等しければ、その整式（方程式）のグラフは一致するということを述べていることになります。

このように考えてくると、前段の前者と後者ともに当たり前のことにように見えます。特に、後者は数式が同じなので当たり前のようですが、ただ、前者は、一つのグラフであっても異なる整式（方程式）での表し方がありえるのかもしれない、という疑問が湧くだろうと思います。しかし、この命題は、整式（方程式）による一つのグラフであれば、整式（方程式）での表し方は一つしかない、ということも主張しているわけです。

このようなグラフによる直観的な解釈は、理解を助けてくれますが証明とは言えないので、次は、その証明の仕方について少し解説を加えたいと思います。

まず、命題１の左から右の証明を考えたときに、$P,Q$は恒等式なので、$x$に$0$を代入しても等式が成り立ちます。つまり、$f(0)=g(0)$であり、したがって、定数項だけが残り$a_0=b_0$は簡単に分かります。そうすると、

$$f(x) = a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1$$
$$g(x) = b_mx^m+b_{m-1}x^{m-1}+\ \cdots\ +b_1x^1$$

であり、

$$(a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_2x^2+a_1)x = (b_mx^m+b_{m-1}x^{m-1}+\ \cdots\ +b_2x^2+b_1)x\ \ \ \cdots\ ①$$

が恒等式として成り立ちます。ここで、単純に$x$を払えるのであれば、同じことを繰り返せば各係数が次々に等しいことが分かり、簡単なのですが、実際にはそうなりません。なぜなら、$x=0$の場合には$x$を単純には払えないからです。つまり、$x=0$の場合には、上述の

$$(a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_2x^2+a_1)$$
と
$$(b_mx^m+b_{m-1}x^{m-1}+\ \cdots\ +b_2x^2+b_1)$$

の部分がたとえ異なっていたとしても、$x=0$なので上述の等式①は成り立ち、この二つの部分が等式であるという条件が導き出せません。すなわち、これが$x=0$の場合には$x$を単純には払えないということです。

一方で、$x \neq 0$の場合には、左右の$x$を払うことはできますが、その場合には$x=0$を代入することができず、$a_0=b_0$のときのように定数項が等しいこと$a_1=b_1$を単純に導くことはできません。

ここがこの命題の証明の難しいところと言えるかと思います。

もちろん、$x \neq 0$の値を代入すれば、たくさんの係数に関する一次方程式を得ることができるので、それを連立方程式として解くという方向性も思い付きますが、一般の整式（方程式）としてこの方針を採用するには少々、高校生の段階での連立方程式についての理解では難しいとも思います。

次に示す証明では、この難点をきちんと回避しています。また、次に示す証明の方法とは異なる方法で、後ほど【ｎ次以下一変数の恒等式の根の個数の十分条件】の証明を終えた後に、３つの別の証明も紹介したいと思います。これら４つの証明は、整式（方程式）の同じ性質を根拠にしているものもあれば、異なる性質を根拠に証明を組み立てているものもあります。そこで、どのような性質を根拠に使っているのか、上述の困難をどのように回避、あるいは、克服しているかに注意してもらえると良いと思います。

それでは、解説が長くなってしまいましたが証明に入りたいと思います。

一変数の恒等式の次数と係数の必要十分条件の証明

【一変数の恒等式の次数と係数の必要十分条件の証明】
証明の大きな流れとしては、まず、命題２から証明を行い、命題２から命題１を導くという方針を取りたいと思います。

やはり、ここでも、

$$P = a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0 = f(x)$$

と置きましょう。

まず、命題２の右から左の証明についてですが、係数がすべて$0$ならば、$x$にどのような値を代入しても各項の和も$0$となるので$P=0$が恒等式となることは自明と言えるかと思います。

次に、命題２の左から右の証明を行いたいと思います。

ここで、仮に$P$の各項の係数の少なくとも一つが$0$ではないという仮定を置きましょう。そうすると、たとえ$a_n$が$0$であっても、それよりも低い次数の項のいずれかに係数が$0$ではない最高次数の項があるはずです。その最高次数の項から改めて$a_n$~$a_0$と係数たちを置き直すことにします。さらに、その$a_n$が負であるならば、$f(x)=0$の両辺に$-1$を掛けて、やはり、改めて$a_n$~$a_0$を置き直すことにします。これで最高次数の項の係数$a_n$は正の数であることが言えます。

さらに、$a_{n-1}$~$a_0$の中で負の数となる係数を取り出して、それを$b_{m}$~$b_l$$(n > m \geq l \geq 0)$と表すことにしましょう（添数はそのままに$a$と$b$を置き換えて表します）。

さて、$f(x)=0$は命題の仮定より恒等式なので、$x \neq 0$の範囲のすべての値について$f(x)=0$が成り立ちます。ここでは、$x \neq 0$の範囲の$x$についてのみ考えたいと思います。

そうすると$x \neq 0$なので、$f(x)=0$の両辺を$x^n$で割ることができ、

$$\frac{f(x)}{x^n} = a_n+\frac{a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0}{x^n} = 0 \ \ \ \cdots ①$$

を導けます。

さらに、

$$\frac{a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0}{x^n} = \frac{a_{n-1}}{x}+\frac{a_{n-2}}{x^2}+\ \cdots\ +\frac{a_{1}}{x^{n-1}}+\frac{a_0}{x^n}$$

が言えます。

そして、$x$の範囲を$x > 0$に絞れば、①を満たすためには、

$$a_n \leq -(\frac{b_{m}}{x^{n-m}}+\frac{b_{m-1}}{x^{n-(m-1)}}+\ \cdots\ +\frac{b_{l+1}}{x^{n-(l+1)}}+\frac{b_l}{x^{n-l}})$$

が必要条件であることが分かります。そうでなければ、$\frac{f(x)}{x^n}$が正の数となり$0$ではなくなってしまうからです。$b_{m}$~$b_l$$(n > m \geq l \geq 0)$が少なくとも一つは存在しなければならないこともここから分かります。ただし、$m$から$l$まで小さくはなりますが、一つづつ小さくなるとは限りません。便宜上、煩雑さを避けるためにこのように書きます。

さらに、$x$の範囲を$x > 1$に絞れば、

$$-(\frac{b_{m}}{x^{n-m}}+\frac{b_{m-1}}{x^{n-(m-1)}}+\ \cdots\ +\frac{b_{l+1}}{x^{n-(l+1)}}+\frac{b_l}{x^{n-l}}) < -(\frac{b_{m}+b_{m-1}+ \cdots +b_{l+1}+b_{l}}{x^{n-m}})$$

が成り立ちます。詳しく説明すると、$m$から$l$まで小さくなるので、それを$n$から引いている分母の$x$のべきは右に行くほど大きくなります。したがって、最も小さなべきは$n-m$になります。$x > 1$なので、同じ$x$であればより小さなべきはより小さな値になります。それが分母にあるので、より小さなべきはその項の絶対値をより大きくします。そのため、$x^{n-m}$とそれ以外のべきを入れ替えれば、その項は元の項よりも絶対値で大きくなります。それを$\frac{b_{m}}{x^{n-m}}$以外の項について行っているので、上式が成り立つことになります。

そうすると、

$$0 < a_n < -(\frac{b_{m}+b_{m-1}+ \cdots +b_{l+1}+b_{l}}{x^{n-m}})$$

が成り立ちます。しかし、$b_{m}+b_{m-1} \cdots b_{l+1}+b_{l}$は定数ですので、十分に大きな$x$を取れば右辺は$a_n$より小さくなります（$b_{m}$~$b_l$が一つの場合にも等号は付きますが同様に考えられます）。つまり、そのような$x$では上記の必要条件を満たせず、$f(x)=0$は成立しません。したがって、$f(x)=0$は恒等式とはならず、これは命題の仮定と矛盾します。この矛盾は、$P$の各項の係数の少なくとも一つが$0$ではないという仮定によるものなので、その否定である$P$の各項の係数はすべて$0$であることが分かりました。「命題２」□

次に、命題１について証明したいと思います。やはり、

$$P = a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0 = f(x)$$
$$Q = b_mx^m+b_{m-1}x^{m-1}+\ \cdots\ +b_1x^1+b_0 = g(x)$$

と置きます。ただし、このとき$a_n$と$b_m$は、$a_n \neq 0$と$b_m \neq 0$を満たす各整式の最高次係数とします。そのような最高次係数がない場合というのは、すべての係数が$0$ということですので、すでに命題２の証明によって正しいことが示されています。

次に、$h(x)=f(x)-g(x)$と置くと、

$$h(x)=0\ \Leftrightarrow\ f(x)=g(x)$$

なので、$P=Q$が恒等式とは、$h(x)=0$が恒等式であることと同値になります。$h(x)$は整式なので、命題２より$h(x)$の各項の係数はすべて$0$であることが分かります。

ここで、$n \neq m$とすると、$h(x)$の最高次係数は$a_n$または$-b_m$となることが分かりますが、どちらも$0$ではないので矛盾します。したがって、$n = m$であり、$P,Q$の次数は等しくなります。

さらに、$h(x)$の各項の係数は$a_i-b_i$($n=m \geq i \geq 0$)と表されるので、$a_i-b_i = 0$であり、$a_i = b_i$($n=m \geq i \geq 0$)となり、$P,Q$の両辺の同じ次数の項の係数は、それぞれ等しいことが分かりました。「命題１」□

ｎ次以下一変数の恒等式の根の個数の十分条件

【ｎ次以下一変数の恒等式の根の個数の十分条件】は高校数学の教科書では、以下のように紹介されています。

「一般に、$P$、$Q$が$x$についての$n$次以下の整式であるとき、等式$P=Q$が$n+1$個の異なる$x$の値に対して成り立つならば、この等式は$x$についての恒等式である。」

恒等式とは、両辺の値が存在する限りすべての$x$で成立する式なので、この命題の意味は、等式$P=Q$が$n+1$個の異なる$x$の値に対して成り立つならば、残りのすべての$x$でも成立するということを主張しているとも言えます。それはつまり、前述と同様にグラフに置き換えて考えると、$n$次以下の整式（の方程式）のグラフは、$n+1$個の異なる$x$の値によって一つに定まるということを主張しています。

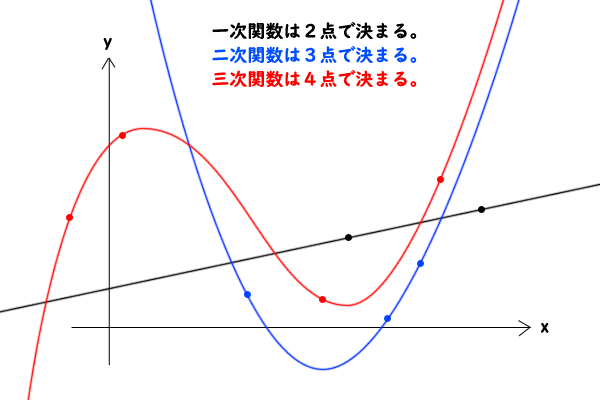
図２：整式（の方程式）のグラフの決定条件

例えば、一次関数ならば２点によって定まると主張しているわけですが、これはユークリッド幾何の「直線は２点によって定まる」という公理と同値であり妥当に感じられると思います。その事実が、２次関数ならば３点、３次関数ならば４点、、、と拡張できるということを述べています。

ｎ次以下一変数の恒等式の根の個数の十分条件の証明

【ｎ次以下一変数の恒等式の根の個数の十分条件の証明】
では早速、証明を行いたいと思います。以下の証明においては、一つの文字に添数が二つ付されていて煩雑と思われるかもしれません。同じ文字を注釈して置き直せば字面は単純になり、慣れている方には分かりやすいのですが、代数の扱いに慣れていない方には難しいところがあります。そのため、煩雑さを避けるよりも正確さを優先して書き下して行こうと思います。

まず、$P-Q=f_n(x)=0$と置きます。そうすると、等式$P=Q$が$x$についての恒等式であることと、$f_n(x)=0$が$x$についての恒等式であることは同値となりますので、これを証明したいと思います。

$P$、$Q$が$x$についての$n$次以下の整式であるので、やはり、$f_n(x)$も$n$次以下の整式です。したがって、

$$f_n(x)=a_{n,n}x^n + a_{n,n-1}x^{n-1} + \cdots + a_{n,1}x^{1} + a_{n,0}$$

と置くことができます。$a$の添数の一番目は、$f_n(x)$の$n$と対応していてこれから次数を下げていくときに用います。$a$の添数の二番目は各項の$x$の指数と対応しています。

ここで、等式$P=Q$、つまり、$f_n(x)=0$が$n+1$個の異なる$x$の値に対して成り立つので、その異なる根（解）を$x_{n,n+1},\ x_{n,n},\ \cdots\ ,\ x_{n,2},\ x_{n,1}$と置きます。$x$の添数の一番目は、やはり、$f_n(x)$の$n$と対応していてこれから次数を下げていくときに用います。$x$の添数の二番目は$n+1$個の異なる根（解）であることを表しています。

次に、$g_n(x)=f_n(x+x_{n,1})$と置きます。そうすると、$g_n(x)$は$f_n(x)$と同じ次数なので、展開して係数について、

$$g_n(x)=a_{n-1,n}x^n + a_{n-1,n-1}x^{n-1} + \cdots + a_{n-1,1}x^{1} + a_{n-1,0}$$

と置くことができます。どうして、$a$の添数の一番目を$n-1$としたのかは続く数行で分かると思います。ここでは、$f_n(x)$と異なる係数であることを押さえて下さい。

そうすると、$x_{n,n+1}-x_{n,1},\ x_{n,n}-x_{n,1},\ \cdots\ ,\ x_{n,2}-x_{n,1},\ 0$は、$g_n(x)=0$の根（解）になります。例えば、$g_n(x_{n,n+1}-x_{n,1})=f_n((x_{n,n+1}-x_{n,1})+x_{n,1})=f_n(x_{n,n+1})=0$が成り立ちます。加えて、$n+1$個の異なる値からその一つの$x_{n,1}$を各々の値から引いただけなので、やはり、$x_{n,n+1}-x_{n,1},\ x_{n,n}-x_{n,1},\ \cdots\ ,\ x_{n,2}-x_{n,1},\ 0$の値もすべて異なります。

ここで、$g_n(0)=a_{n-1,0}=0$と分かります。そこで、

$$g_n(x)=a_{n-1,n}x^n + a_{n-1,n-1}x^{n-1} + \cdots + a_{n-1,1}x^{1} = 0$$

について、$x_{n-1,n+1},\ x_{n-1,n},\ \cdots\ ,\ x_{n-1,3},\ x_{n-1,2}$を$x_{n-1,n+1}=x_{n,n+1}-x_{n,1},\ x_{n-1,n}=x_{n,n}-x_{n,1},\ \cdots\ ,\ x_{n-1,3}=x_{n,3}-x_{n,1},\ x_{n-1,2}=x_{n,2}-x_{n,1}$と置くと、$x_{n-1,n+1},\ x_{n-1,n},\ \cdots\ ,\ x_{n-1,3},\ x_{n-1,2}$は上式の$n$個の異なる根（解）になります。その上、すべて$0$ではないので、$x$を払った式について、

$$f_{n-1}(x)=a_{n-1,n}x^{n-1} + a_{n-1,n-1}x^{n-2} + \cdots + a_{n-1,2}x^{1} + a_{n-1,1}$$

と置くと、やはり$x_{n-1,n+1}\ ,x_{n-1,n},\ \cdots\ ,\ x_{n-1,3},\ x_{n-1,2}$は$f_{n-1}(x)=0$の$n$個の異なる根（解）になっています。ここまで来て、最初の$f_{n}(x)$に対する条件と比較すると、次数と根（解）の個数が一つ下がっているだけということが分かると思います。

したがって、この操作を繰り返し、次数を下げて行くと必ず以下の次数にまで下がるはずです。

$$f_{1}(x)=a_{1,n}x + a_{1,n-1}$$

そして、$x_{1,n+1},\ x_{1,n}$は$f_{1}(x)=0$の$2$個の異なる根（解）になります。

そうすると、最後に$g_1(x)=f_1(x+x_{1,n})$とおき、展開して係数について、

$$g_1(x)=a_{0,n}x + a_{0,n-1}$$

とおくと、$g_1(0)=f_1(0+x_{1,n})=0$より、$a_{0,n-1}=0$が分かります。そこで、

$$g_1(x)=a_{0,n}x = 0$$

にいて、$x_{0,n+1}$を$x_{0,n+1}=x_{1,n+1}-x_{1,n}$と置くと、$x_{0,n+1}$は上式の$1$個の$0$ではない根（解）になります。そうすると、

$$a_{0,n}x_{0,n+1} = 0$$

が成り立ち、$x_{0,n+1} \neq 0$より、$a_{0,n}=0$となります。したがって、$g_1(x)$は、すべての係数が$0$なので$x$について恒等式であることが分かりました。

そうすると、$f_1(x+x_{1,n})=0$も恒等式だと分かります。ここで、任意の$x$について$t=x-x_{1,n}$とおけば、すべての$x$について$f_1(x+x_{1,n})=0$は成り立つことから、$t$を代入しても成り立つはずなので、$f_1(t+x_{1,n})=f_1(x-x_{1,n}+x_{1,n})=f_1(x)=0$が成り立ちます。結局、$f_1(x)=0$が恒等式であることが分かりました。これは、グラフで考えれば$x$軸の向きに$x_{1,n}$だけ平行移動することなので、$x$軸が$x$軸上で平行移動してもやはり$x$軸であることは自明のことと言えます。

$f_1(x)=0$が恒等式ならば、$g_2(x)=f_1(x) \cdot x=0$も恒等式です。$g_2(x)=0$が恒等式なら上記と同様に考えて$f_2(x)=0$も恒等式です。このように繰り返して考えて行けば、次数をさかのぼり$f_n(x)=0$が恒等式であることが分かります。したがって、等式$P=Q$が$x$についての恒等式であることが分かりました。□

一変数の恒等式の次数と係数の必要十分条件の別証

冒頭で述べましたように【一変数の恒等式の次数と係数の必要十分条件】の別の証明をいくつか挙げたいと思います。命題２から命題１を証明することはすべて同じとして、命題２の左からの右への別証を挙げることにします。

発散する性質を使って

前述した【一変数の恒等式の次数と係数の必要十分条件】の命題２の証明は、一次以上の整式（方程式）であれば$x$をどんどん大きくしていけば、正または負のどちらかに必ず発散するという性質を上手く取り出して、極小において使っているとも言えます。その方が極限に対する理解がさほどなくとも分かりやすいと思ったからです。

ただ、極限に対する理解がきちんとあればこの性質を直接、用いる方が分かりやすいかもしれません。つまり、正または負のどちらかに必ず発散するのなら$f(x)=0$は恒等式ではありえないということです。実際に、以下のように$x^n$を括りだして$x$の極限を取れば良いことになります。

$$f(x) = x^n(a_n+\frac{a_{n-1}}{x^{1}}+\ \cdots\ +\frac{a_1}{x^{n-1}}+\frac{a_0}{x^n})$$

$a_n > 0$について考えると、$x \rightarrow +\infty$を取ると、極限値の和と積より、特に括弧内は$a_n$に収束するので、$f(x) \rightarrow +\infty$となります。ここで、$+\infty$に発散するということは、任意の$y > 0$についてある$x$が存在して$f(x) > y$が成り立つということなので、$f(x) \neq 0$を満たす$x$が存在するということになります。したがって、$f(x)$は恒等式にならないことが分かりました。$a_n < 0$についても同様に考えることができます。□

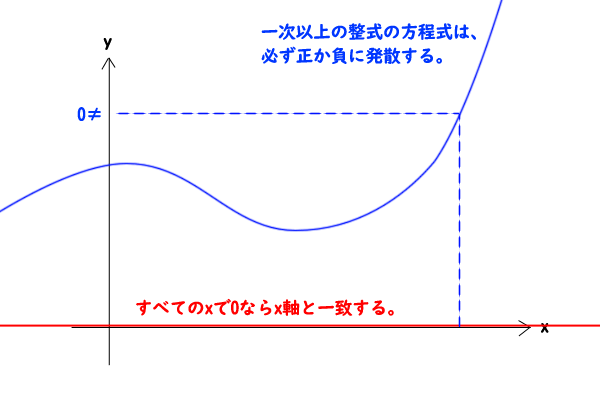
図３：一次以上の整式（方程式）の発散

上記の発散の議論について理解しにくい方は、集合による二項定理と多項定理の証明とパスカルの三角形：一般の有限な集合と自然数の集合、特にその中の余談：無限、極限の定義を参考にしてみて下さい。有限と無限の違いなどが解説されています。次の【連続性を使って】の証明にも必要な理解となります。

連続性を使って

【変数の恒等式の必要十分条件の解説】で説明した通り、

$$f(x) = a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0=0$$

について、$f(0)=a_0=0$なので、

$$f(x) = (a_nx^{n-1}+a_{n-1}x^{n-2}+\ \cdots\ +a_2x^1+a_1)x=0$$

と変形でき、

$$g(x) = a_nx^{n-1}+a_{n-1}x^{n-2}+\ \cdots\ +a_2x^1+a_1$$

とおくと、$x \neq 0$のときは、$g(x)=0$が言え、$x = 0$のときは、$g(x)=0$とは必ずしも言えないのが難点でした。そこで、$x = 0$のときに、つまり、$g(0)=a_1 \neq 0$と仮に置いて、矛盾を導き出したいと思います。

この証明は、整式（の方程式）の連続性を使って証明を行うため、連続性について勉強をまだしていない方には理解しずらいと思い別証としました。関数の連続性とは、簡単なイメージを述べると「関数がつながっている」ということであり、逆に、飛び飛びに切れたりしていないということを意味します。

直観的には$x = 0$のときに$g(0) \neq 0$で、$x \neq 0$のとき$g(x)=0$では、$x = 0$の近くで飛び飛びに切れるしかなく、それでは整式（の方程式）の連続性に矛盾するだろう、ということを言いたいのですが、正確に表現するには連続性についての理解が必要になります。

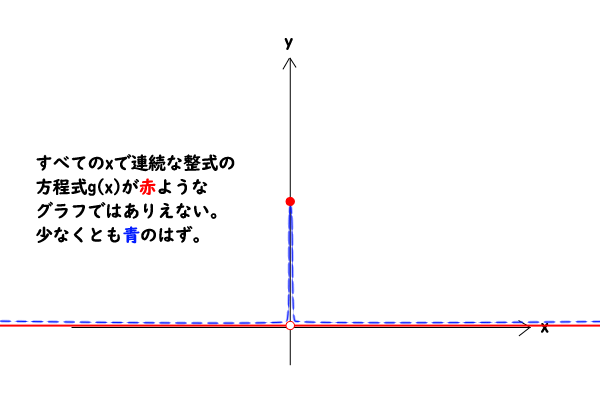
図４：整式（の方程式）の連続性

関数の連続性の基本的な性質として、連続な関数と関数の和・定数倍・積はやはり連続という命題が成立します。そこで、$x$は連続であることから、その和・定数倍・積で組み立てられている整式もやはり連続であるということが分かります。そうすると、$g(x)$もすべての$x$について連続であることが分かります。

ここで、$g(0)=a_1 \neq 0$が仮定されているので、くわえて$x=0$おいて$g(x)$は連続なので、どんなに小さな$y > 0$についても$|a_1 – g(x’)| < y$を満たす、$x=0$に非常に近い$x’ \neq 0$が取れることが分かります。つまり、$g(x’) \neq 0$となる$x’ \neq 0$が存在することになります。しかしながら、これは$x \neq 0$のときは、$g(x)=0$である事実と矛盾します。したがって、$g(0)=a_1 = 0$、つまり、$x = 0$のときも$g(x)=0$でなければならないということが分かりました。□

微分可能性を使って

整式（の方程式）が微分可能であることを知っているならば最も簡単な証明は微分を取ることです。すべての$x$について、

$$\begin{eqnarray} f(x) & = & a_nx^n+a_{n-1}x^{n-1}+\ \cdots\ +a_1x^1+a_0 = 0 \nonumber \\ f^1(x) & = & a_n\cdot nx^{n-1}+a_{n-1}\cdot (n-1)x^{n-2}+\ \cdots\ +a_2\cdot 2x^1+a_1 = 0 \nonumber \\ f^2(x) & = & a_n\cdot n(n-1)x^{n-2}+a_{n-1}\cdot (n-1)(n-2)x^{n-3}+\ \cdots\ +a_3\cdot 3\cdot 2x^1 +a_2\cdot 2\cdot 1 = 0 \nonumber \\ & \cdot & \nonumber \\ & \cdot & \nonumber \\ f^n(x) & = & a_n\cdot n! = 0 \nonumber \end{eqnarray}$$

が成り立ちます。$P=f(x)=0$は恒等式なので、その任意回数の導関数もやはりすべての$x$について$0$であることが必要条件であるからです。グラフで考えれば、$x$軸を何度微分した導関数も$x$軸になるということです。したがって、各式に$x=0$を代入すれば、すべての係数が$0$であることが求められます。□

発展：線形代数や代数学の基本定理との関連

【一変数の恒等式の次数と係数の必要十分条件の証明】と【ｎ次以下一変数の恒等式の根の個数の十分条件の証明】とは、どちらも係数に関する連立一次方程式の根（解）の問題に帰結することができるので、大学の初等で学ぶ線形代数の知識を用いればこのページの内容よりも見通し良く証明を組み立てることができると思います。

線形代数は、簡単に言えばベクトルや行列についての数学分野です。数学全体はもちろんのこと、科学全般にも応用が広く微分積分を扱う解析学と並び、今日の科学技術の基礎になっている数学分野です。したがって、大学の理系学部に入学すれば線形代数と解析学は、各学部の数学的な基礎として修学を要求されることになり、その後の研究や仕事の土台となります。

数学には、応用の広い基礎的な数学分野において、その中でも基本となる重要な定理を○○の基本定理と呼ぶ慣習があります。例えば、算術の基本定理、代数学の基本定理などです。このページの内容は、代数学ですので代数学の基本定理と深く関連しています。例えば、以下に述べるように代数学の基本定理から【ｎ次以下一変数の恒等式の根の個数の十分条件】は導くことができます。

代数学の基本定理とは、「複素係数（したがって実数係数も）の$n \geq 1$ 次方程式は複素根を持つ」あるいは「複素係数の$n \geq 1$ 次方程式は複素根を重複を含めて丁度$n$個持つ」という命題です。後者は前者より導かれ、使い勝手が良いのでこちらを代数学の基本定理として言及する場合もあります。完全な証明はガウスによって初めて与えられたようです。易しいものから難しいものまで様々な証明法が発見されていますが、簡単なものでも大学初等の知識は必要です。例えば、「基礎数学１ 線型代数入門　斎藤正彦著」に掲載されています。

代数学の基本定理によると、$n \geq 1$ 次方程式は複素根を重複を含めて丁度$n$個持つので、異なる根（解）は多くとも$n$個以下しか持ちえません。しかしながら、【ｎ次以下一変数の恒等式の根の個数の十分条件】からは、$n$ 次以下の方程式が$n+1$個の異なる根（解）を持つこと、これが必要条件となります。したがって、$n$は$n \geq 1$ ではありえず、$n = 0$となります。その上、$n = 0$で$f(x)=0$を満たすには、$f(x)$が恒等的に$0$となるしかありえない、ということになります。このように【ｎ次以下一変数の恒等式の根の個数の十分条件】が簡単に証明できてしまいました。代数学の基本定理の重要性を少し実感できましたでしょうか。

ここで、注意してもらいたいのは代数学の基本定理は、複素係数であって実数係数も含みますが実数係数に限定はされていないことです。したがって、前段の証明より、【ｎ次以下一変数の恒等式の根の個数の十分条件】の係数と$x$の範囲は複素係数でも成立します。前々章の【ｎ次以下一変数の恒等式の根の個数の十分条件の証明】も恐らく吟味はしていませんが、係数と$x$の範囲を複素係数と想定しても成立すると思います。結構、拡張のできそうな枠組みにも見えてくるのが興味深い点かと思います。

あと、【ｎ次以下一変数の恒等式の根の個数の十分条件】は、$n$ 次以下の整式（方程式）のグラフは、$n+1$個の異なる$x$の値によって一つに定まるということを主張していると前述しましたが、これは代数学の基本定理が、$n$ 次以下の整式（方程式）のグラフの決定にも大きく関連していることを示しています。

例えば、$n$ 次の整式（方程式）のグラフの$m$個の点を取り、この$m$個の点を共有する$n$ 次の整式（方程式）のグラフを考えたときに、$m=n+1$ならば上記より一致しかありえないわけですが、$m \leq n$個の場合はどうか、どのような$n$ 次の整式（方程式）のグラフがありえるのかと考えてみると面白いと思います。

代数学の基本定理と整式の割り算と余りの一意性より、$n \geq 1$ 次の整式（方程式）は重複を含めて$n$個の複素根で因数分解できることをまず求め、それを使って考えていくのがポイントだろうと思います。

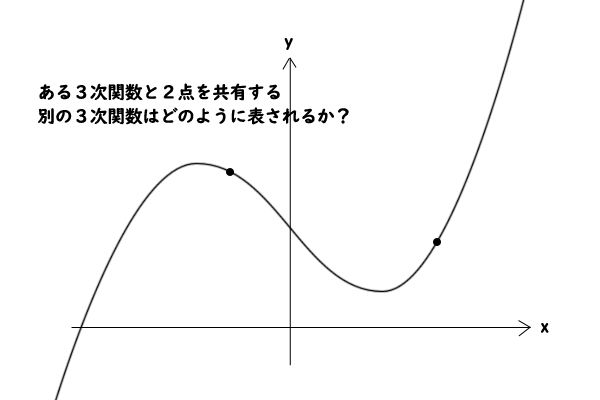
図５：整式（の方程式）の共有点

著者：L&M個別オンライン教室　瀬端隼也
公開日：２０２０年１２月４日
修正日：２０２１年５月３１日　第５章『発展：線形代数や代数学の基本定理との関連』の第４段落「代数学の基本定理とは、～」に「複素係数（したがって実数係数も）の$n \geq 1$ 次方程式は複素根を持つ。」、「後者は前者より導かれ、使い勝手が良いのでこちらを代数学の基本定理として言及する場合もあります。」を追加・修正しました。