集合による二項定理と多項定理の証明とパスカルの三角形

【目次】
０．はじめに
 １．集合による順列と組合せの理解
　　１－１．一般の有限な集合と自然数の集合
　　　　１－１－１．離散的な集合と連続的な集合
　　　　　　１－１－１－１．一対一対応という比較法
　　　　　　１－１－１－２．点と直線、有理数と実数の違い
　　　　１－１－２．有限、無限、一般の有限な集合
　　　　　　１－１－２－１．一般の有限な集合の定義
　　　　　　１－１－２－２．順序や大きさと要素数の違い
　　　　　　１－１－２－３．余談：無限、極限の定義
　　　　１－１－３．一般の有限な集合と順列や組合せ
　　１－２．順列の集合
　　　　１－２－１．n個の順列
　　　　１－２－２．n個からr個を取り出した順列
　　１－３．組合せの集合
　　　　１－３－１．n個からr個を取り出した組合せ
 ２．二項定理
　　２－１．展開された各項の順列
　　２－２．添数を消した各項の順列
　　２－３．一般の順列の集合との対応関係
　　２－４．教科書の証明との違い
 ３．パスカルの三角形
　　３－１．二項定理との対応
　　３－２．平面座標の道順との対応
 ４．多項定理
 ５．発展：多項定理と道順とパスカルの三角形
　　５－１．多項定理と多次元座標の格子点の道順
　　５－２．多次元に拡張されたパスカルの三角形
　　５－３．自然数のべき乗と多次元座標の格子点の道順
　　５－４．フェルマー・ワイルズの定理と格子点と道順
　　　　５－４－１．数学で身に付く重要な考え方
　　５－５．自然数と格子点の興味深い関係

はじめに

高校数学の教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）では、数学Ａの「場合の数と確率」という単元で、場合の数から積の法則を学んで、積の法則を使って順列の計算方法を学び、さらに組合せの計算方法も学びました。そして、この数学Ａの単元「場合の数と確率」の冒頭では、数Ⅰで学んだ集合についての、特に集合の要素の数についての計算規則を改めて学び、場合の数の数え上げに生かせるような構成が取られています。

このページで解説する内容が掲載されている数学Ⅱでは、単元「式と証明」の冒頭で$(a+b)^{n}$の展開式、つまり、二項定理を学びます。教科書は、パスカルの三角形に始まり、組合せを用いて二項定理を解説し、さらに、研究において$(a+b+c)^{n}$の展開式、つまり、多項定理を解説しています。このように、教科書の通りにですが、二項定理は、場合の数、順列、組合せと密接に関わっており、その理解のためには場合の数、順列、組合せを集合を用いて正確に考えられることが大切になります。

そもそも、場合の数、順列、組合せは、小学生や中学生の頃から学んできた事柄かと思いますが、高校数学では集合を用いて考え始めることや、場合の数、順列、組合せを確率の基礎として学び、確率の多少なりとも複雑な概念を扱い始めることが、小学生や中学生との違いになるかと思います。（参照：集合による場合の数と確率の考え方）

しかしながら、実際には、教科書もそうですが、集合の基本的な概念を学ぶだけで多くの生徒は手一杯になり、それを場合の数、順列、組合せ等に適用する段階、つまり、集合を用いて正確に考える所までにはなかなか手が伸ばせない現状があるようです。

集合とは、数学で取り扱う題材の共通の特徴を取り出した型枠のようなもので、集合自体のことを考えることも大切ですが、それを各数学の分野で活用することで各分野の見通しが良くなり理解が深まるという効果の方が重要になります。集合を学んで各分野で活用しないというのは、憲法を学んで各法律の分野でその原理を無視することと論理的には同じで、結局、原理を学んだ意味や価値がないということになります。

具体的には、小学生や中学生の頃から何となく学んできた順列や組合せを、論理的に理解するためには、集合をきちんと用いて行くことが欠かせない作業になります。二項定理の展開式と組合せの本質的な繋がりも、集合を用いて両者を整理することで初めて理解することができると思います。

したがって、このページでは、改めて一般的な集合をちょっと浅堀した復習から始めて、順列や組合せを明確に集合として表わし、それから二項定理、パスカルの三角形、多項定理も集合を用いて整理し、それぞれの関係性を解説して行きたいと思います。

集合による順列と組合せの理解

一般の有限な集合と自然数の集合

順列や組合せを論理的に理解するためには、集合をきちんと用いて行く必要があると述べました。それは、順列や組合せを一般の集合において定義していけば、余計な情報を排除してすっきりと見通し良く順列や組合せを考えることができるからです。

ただ、順列や組合せを一般の集合において定義していくといっても、このページでは、一般の”有限な”集合においてのみ定義して行きたいと思います。有限でない集合とは、無限の要素を持った集合ということになりますが、無限にある要素の順列や組合せを考えるのはなかなか難しそうなので、まずは、一般の有限な集合に限って考えようということです。

それでも、一般の有限な集合とは何か、特に、有限とは何か、そしてそれに対する無限とは何か、ということを考え始めると、それだけでもなかなか難しい話です。この難しさは当然のことで、逆に集合という考え方が発見されるまでは有限、無限とは何か、ということを明確にすることを人類ができていたのかというと、それほど明確な理解をできていたわけではなく、明らかに集合という考える道具の登場によって、有限、無限に関する概念は明確化されていきました。

それは自然なことで、というのは先に、集合とは数学で取り扱う題材の共通の特徴を取り出した型枠のようなものと言いましたが、少し難しいですがこれを正確に表現すると、集合とは数学で扱う対象の共通の特徴を抽象した概念と言えます。そして、数学で扱う対象とは、その必要条件は、概ね「数」と何らかの関係を有した対象です。したがって、集合が数と密接な関係を持っているのは当然であり、その密接な関係を用いて数をより深く理解する、つまり、集合を用いて数をより深く理解できる、という流れは自然なことと言えると思うのです。

そして、物事の関係というのは、多くが片一方の関係ではなく相互的な双方向のものであり、逆に言うと、集合をより深く理解するためには数をより深く理解することも必要になります。つまり、集合を用いて数をより深く理解することは、集合をより深く理解することにも繋がるわけです。

したがって、集合をきちんと用いて行くためには、その肝とも言える有限、無限、一般の有限な集合とは何かを明確に理解しておくことが必要だろうと感じます。そのため、まずは、説明が長くなってしまいますが、割愛するか分割すべきか悩んだのですが、とても重要な話で応用の広がる内容なので、集合の持つ量的な性質についての話から解説を始めたいと思います。

離散的な集合と連続的な集合

カントールが集合を見つけ出し（参照：集合と命題について）、それが数学者たちに受け入れられる最も大きな動機になったのは、離散的な集合と連続的な集合の違いを明確にすることができたからです。この離散的な集合と連続的な集合の意味は後ほど分かります。

一対一対応という比較法

その考え方のポイントは、異なる集合の要素を一対一に対応することができるか否かで、異なる集合の量を比較するところにありました。この一対一対応の比較方法は、それまでの人類が持つ量的な感覚とは少し異なるものでした。

例えば、要素数が1個と２個の集合では、要素間に一対一対応を付けることはできません。これは１個よりも２個が多いという通常の量的感覚です。次に、偶数$2n$と奇数$2n-1$の集合を考えてみましょう。$n$が等しい要素同士を対応させれば、互いのすべての要素について一対一対応を取ることが出きます。ここまでも通常の量的感覚で納得できそうです。しかし、さらに自然数$n$と偶数$2n$の集合を考えてみましょう。偶数$2n$と奇数$2n-1$の集合と同様に、$n$が等しい要素同士を対応させれば、互いのすべての要素について一対一対応を取ることが出きてしまいます。

ここで、一対一対応とは、互いのすべての要素について漏れもなく重なりもなく要素と要素の組を一通りに定めることができるということです。具体的には、$n=1$：$(1,2)$, $n=2$：$(2,4)$, $n=3$：$(3,6)$, $n=4$：$(4,8)$, … とたしかに、（自然数,偶数）の一通りの組を定めることができ、第一列目にはすべての自然数が漏れも重なりもなく入っており、第二列目にもすべての偶数が漏れも重なりもなく入っています。

こうして、カントールは一対一対応という比較方法においては、自然数$n$と偶数$2n$も量的に等しいとみなせることに気付きました。そして、さらに自然数と有理数、有理数と実数を比較していくと、驚くべきことに自然数と有理数までは一対一対応を取ることができ、自然数と実数は一対一対応を取ることができないという結論を得ました。この時にカントールが用いた証明方法を「カントールの対角線論法」と呼びます。興味のある方は、高校生でも”頑張れば”理解できる内容なので調べてみて下さい。ただ、大学範囲であることと話が逸れ過ぎるので、ここでは紹介を割愛します。

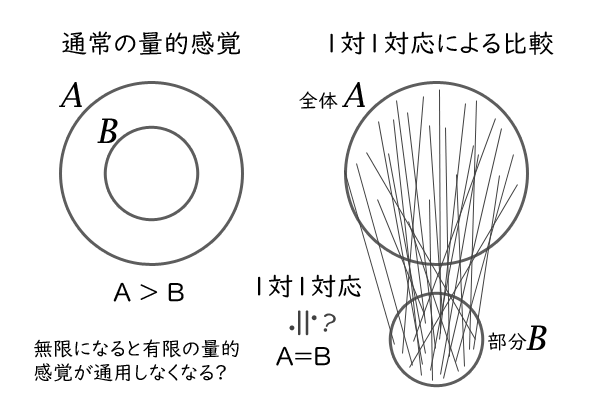
図１：通常の量的感覚と一対一対応による比較法

このことは、通常の量的感覚と反するような点、先に挙げた自然数$n$とその真部分集合であるはずの偶数$2n$の集合が一対一に対応できる、つまり、部分と全体であっても量的に等しいものと扱われてしまうというおかしな点もあれば、一方で、幾何学的な直観と整合する点もあります。

点と直線、有理数と実数の違い

例えば、半直線上の起点を０として自然数の長さにある点を集めた集合$A$と、正の有理数の長さにある点を集めた集合$B$と、正の実数の長さにある点を集めた集合$C$を考えてみます。ピタゴラス以来、集合$A$はもちろんですが、集合$B$にも入らない点が半直線上にあることが知られており、それを無理数と呼び、有理数に無理数を加えた数の集合を実数と呼ぶのでした。

図２：自然数、有理数、実数の違い

つまり、幾何学的な直観として、半直線上のすべての点の集合を集合$D$とすると、集合$A$と集合$B$は、集合$D$との間に一対一対応を取れそうにないのですが、集合$C$は、集合$D$との間に一対一対応を取れそうなのです。さらに言い換えると、実数で直線上の点をすべて表すことはできるけれど、自然数や有理数では無数に点があってもそれはできない。この幾何学的な直観とカントールが示した集合の一対一対応の比較法による量的境界線は、見事に一致していたのです。

そこで、実数の集合と一対一対応を取ることができる集合を連続的な集合、対して自然数や有理数の集合と一対一対応を取ることができる集合を離散的な集合と表現することができます。正確には、離散的な集合を可算集合、連続的な集合を非可算集合と呼びます。簡単に言うと、前者は数えられる集合、後者は数えられない（ほど多い）集合です。数えられるとは自然数と一対一対応を取れるということです。

ちなみに、上記の「連続」という用語は、数学Ⅲの単元「極限」で紹介される「関数の連続性」とは、扱う対象と定義が異なります。ここでの対象は集合であり、後者の対象は関数です。ただ少なくとも、実数の範囲であれば、すべての点で繋がっているという直観的な特徴はどちらにもあてはまっています。

これらの数学用語としての正確な定義は、大学の各数学分野で異なる視点で扱われることになるかと思いますが、基本的な語義のイメージとしては、連続的な対象とはどこまで拡大しても各要素が繋がっていて数えられないほどある対象で、離散的な対象とは遠目に縮小すると密に見えるほどあったとしても実際には各要素が離れていて数えられるほどしかない対象と捉えて良いかと思います。

現代科学においても、例えば水を大局的に扱うには前者の連続的な対象のように流動性のある物体として捉える方が扱いやすく、しかし、局所的には、原子が構成単位になっているので後者の離散的な対象のように捉える必要があり、また、さらに個別の原子の振る舞いは波のようで確率的には前者の連続的な対象のようであり、と様々な場面でこれらの概念が適切に用いられます。

少し脱線しましたが、以上のポイントを整理すると通常の量的感覚は、有限の場合には数え上げで量を比較し、無限の場合には部分と全体で全体の方が部分より多いだろうと推論するのに対して、カントールの一対一対応という比較方法によると、有限の場合は同じですが、無限の場合には部分と全体で全体の方が部分より多いだろうという通常の量的感覚の前提が認められない代わりに、同じ無限であっても離散的な数えられる量と連続的な数えられない量を明確に区別することができます。

つまり、通常、「一対一対応」と「部分と全体」という二つの尺度を用いて量的比較するところを、カントールは「一対一対応」の原理のみを採用するという基準転換を行ったとも言えます。

有限、無限、一般の有限な集合

ここでやっと、有限、無限、一般の有限な集合とは何かという話に戻りたいと思います。つまり、上記の説明から分かる通り、連続的な集合ならば少なくとも無限個の要素を含んでおり、したがって、一般の有限な集合とは、少なくとも離散的な集合です。さらに、そこから分かることは、一般の有限な集合は離散的な集合なので、数えられる量を持ち自然数の部分集合と一対一対応を取れるということです。

一般の有限な集合の定義

そして、さらに、それが一般の有限な集合の定義となりえます。つまり、一般の有限な集合とは、「自然数の部分集合と一対一対応を取れて、その対応する自然数の部分集合に最大数があるもの」、と定義することができます。このように定義することで、集合の要素数としての有限とは、漠然と限られた量のものという意味ではなく、自然数という明確化された概念で基礎付けられることになります。

順序や大きさと要素数の違い

ちなみに、集合の要素数としての有限性と、集合の要素の持つ順序や大きさとしての有限性の違いを意識することは大切だろうと思います。例えば、自然数は、最大数によって上限が定まれば集合の要素数としても有限になりますが、正の有理数は、最大数又は最大値によって上限が定まっても集合の要素数として有限になるとは限りません。つまり、ここでは、この自然数の順序としての有限性と要素数としての有限性が同値であるという特徴を、一般の有限な集合の定義に援用したということになります。

余談：無限、極限の定義

さらに余談ですが、有限に対する、無限、と言っても可算集合（数えられる集合）の無限の定義は、「自然数の部分集合と一対一対応を取れて、その対応する自然数の部分集合に最大数がないもの」、と定義することができます。ここから、大学以降では、”極限”、つまり”無限”を扱う際に「任意の自然数$n$について、$n$より大きな$N$が必ずある（したがって、最大数はない）場合」という自然数の無限の定義と同値な条件を用いることが多くなります。そして、集合論において面白いのはここからで、無限という量にも区別が付けられるという話だと思うのですが、その話はこれ以上は取り上げません。

ここからの話は、一般の有限な集合に限っていきますが、だからといって以上の考察が無益になるわけではなく、無限について視野を広げることによって、有限とは何かということも理解できるのであって、一般の有限の集合を自然数によって定義付けできたことは、以降の順列と組合せの理解を深めるためにも非常に有益であることが分かってくると思います。

一般の有限な集合と順列や組合せ

それでは、順列や組合せを論理的に理解するために、順列や組合せを一般の有限な集合$G$において定義していこうと思います。といっても、やはり、いきなり一般の有限な集合$G$と言われてもピンと来ないかもしれませんので、具体例を挙げると、$G={a, b, c, \cdots, x, y, z}$などをイメージすると良いと思いますし、それ以外にも人の名前でも、国の名前でも、「自然数の部分集合と一対一対応を取れて、その対応する自然数の部分集合に最大数があるもの」を想像すれば良いわけです。

特に、一般の有限な集合$G$とは、「自然数の部分集合と一対一対応を取れて、その対応する自然数の部分集合に最大数があるもの」なので、「自然数の部分集合で最大数があるもの」、それ自身も集合$G$の具体例であることがポイントです。

くわえて、この定義から、どのような有限な集合も「自然数の部分集合で最大数があるもの」、例えば${1,2,3, \cdots, n-1, n}$と一対一対応を付けることができるので、一対一対応で定まった一通りの組に従ってその要素と${1,2,3, \cdots, n-1, n}$をいつでも置き換えることができることになります。

それは、有限な集合から順列や組合せを作成してから置き換えても、置き換えてから順列や組合せを作成しても、その置き換えの規則である一通りの組は変わらないので、結果は何も変わらないということになります。つまり、どのような有限な集合もその要素を${1,2,3, \cdots, n-1, n}$で置き換えて、順列や組合せを考えても良いということが分かります。

さらには、ある有限な集合から順列や組合せを考えるということは、一対一対応を付けることができるので、自然数の集合に置き換えて考えることのできる他の有限な集合で考えても同じこと、ということになります。

この点が、一般の有限な集合の定義を明確にしたメリットになります。したがって、ここからは${1,2,3, \cdots, n-1, n}$の順列や組合せだけを考えることにしましょうと言いたいところなのですが、表記上の問題から${1,2,3, \cdots, n-1, n}$の順列や組合せを考えることは、誤記や誤解を生む可能性が多くなりますので、以降では、基本的に添数付きアルファベット$G=\{a_{1}, a_{2}, a_{3}, \cdots, a_{n-1}, a_{n}\}$を使って、順列や組合せを考えていくことにしたいと思います。

順列の集合

n個の順列

一般の有限な集合$G=\{a_{1}, a_{2}, a_{3}, \cdots, a_{n-1}, a_{n}\}$の$n$個の順列の集合とは、$G$から一つづつ要素を順番に取り出して並べたものを要素とする集合です。この順列の集合を$P$とすると、

つまり、
\[P=\{\ a_{1}a_{2}a_{3} \cdots a_{n-1}a_{n},\ \ \ a_{1}a_{2}a_{3} \cdots a_{n}a_{n-1},\ \ \ \cdots \ \ \ , a_{n-1}a_{n}a_{n-2} \cdots a_{2}a_{1}, \ \ \ a_{n}a_{n-1}a_{n-2} \cdots a_{2}a_{1}\ \}\]
です。

頭の体操のために、「一つづつ要素を順番に取り出して並べたもの」を少し難しく考えると、「順番に並べる」とは初めから終わりまで順序を付けるという意味であり、加えて、「一つづつ」それを行うわけなので、すべての要素の間に順番を付けることになります。それはつまり、自然数で数え上げるということに他なりません。さらに、「一つづつ要素を取り出して」、それを行うということは$G$からの写像（下記の【注意】を参照のこと）であると捉えることができ、自然数の集合を$N$とすると、順列とは$G \rightarrow N$の写像であり、それも一対一対応（全単射）であることが分かります。

【注意】写像とは、ある集合とある集合の要素の間に定義された対応のことです。対応とは、要素と要素の方向付きの組、あるいは、組です。例えば$a \rightarrow b$あるいは$(a,b)$と考えてください。関数と同じで、ある集合を定義域とし、ある集合を値域とします。定義域となるすべての要素について、その対応が定義されていて、かつ、定義域の一つの要素に値域の一つの要素のみが対応する、ことが通常の写像の必要条件となっています。関数は数を対象（集合の中身）とした写像であり、写像は関数の集合における一般化と言えます。2003年までは、高校数学でも教えられていたようです。なぜ、こんなものを考えるかというと、このページを読むと分かるように、集合と集合の間の対応関係を整理することができるからです。【注意終了】

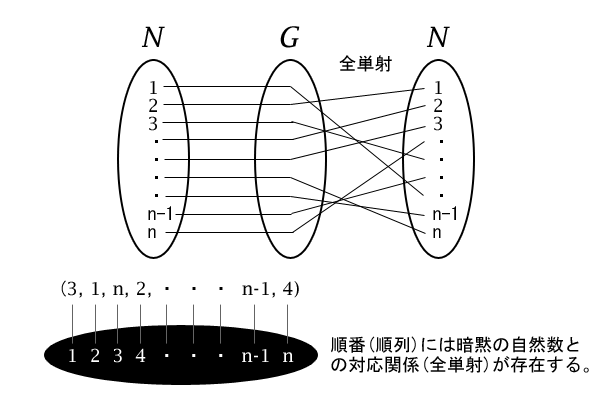
N→Nへの一対一対応の写像
図３：$N \rightarrow N$への一対一対応の写像

もともと、一般の有限な集合$G$は$N$に置き換えて考えても良いと前章で分かっているので、順列とは$N \rightarrow N$への一対一対応の写像（全単射写像）と言えることが分かりました。つまり、$n$個の自然数の順番$( 1, 2, 3, \cdots, n-1, n )$を入れ替えたもの、例えば$( n, n-1, n-2, \cdots, 2, 1 )$や$( 2, 1, 3, \cdots, n-1, n )$で表すことができます。これは簡単に考えれば、「順列とは順番、順番を入れ替えたもの」という小中学校で学ぶ当たり前の事実の再確認と言えます。

順列の集合$P$の要素数は、数学Ａ「場合の数」で学んだ積の法則（参照：集合による場合の数と確率の考え方：積の法則）により、先頭から取りえる要素の場合が$n$通り、その各々の場合について$n-1$通り、その各々の場合について$n-2$通り、、、その各々の場合について$2$通り、その各々の場合について$1$通りあるので、$n!=n\cdot n-1\cdot \cdots \cdot 2\cdot 1$で計算できるのでした。

n個からr個を取り出した順列

$n$個から$r$個を取り出した順列とは、一般の有限な集合$G=\{a_{1}, a_{2}, a_{3}, \cdots, a_{n-1}, a_{n}\}$で考えると、$G$から一つづつ要素を順番に取り出して$r$個並べたものを要素とする集合です。つまり、一般の有限な集合$G$の$r$個の順列の集合です。前節では、集合$G$のすべての要素$n$個を取り出していたところを、$r$個しか取り出さないということです。この集合を$PR$と書きましょう。

したがって、集合$P$の要素である$n$個並べた順列の後方$n-r$個を並べない、削除した順列が集合$PR$の要素になるということです。つまり、
\[PR=\{\ a_{1}a_{2}a_{3} \cdots a_{r-1}a_{r},\ \ \ a_{1}a_{2}a_{3} \cdots a_{r}a_{r-1},\ \ \ \cdots \ \ \ , a_{n-1}a_{n}a_{n-2} \cdots a_{n-r+2}a_{n-r+1}, \ \ \ a_{n}a_{n-1}a_{n-2} \cdots a_{n-r+2}a_{n-r+1}\ \}\]
となります。ただ、集合$P$の先ほど示した要素についてのみ記述しただけで、すべての要素を整列して書き下せているわけではないことに注意してください。

そうすると、集合$P$の要素において考えると、削除した後半の$n-r$個の順列の部分は異なるけれど、削除しなかった前半の$r$個の部分は等しいという順列が複数あります。集合$PR$では、そのような前半の$r$個の部分が等しい順列を一つの要素とみなすわけです。このことを写像として捉えると、$P \rightarrow PR$の写像で、集合$P$の要素からその要素の「前半の$r$個の部分と等しい」集合$PR$の要素への写像とみなすことができます。

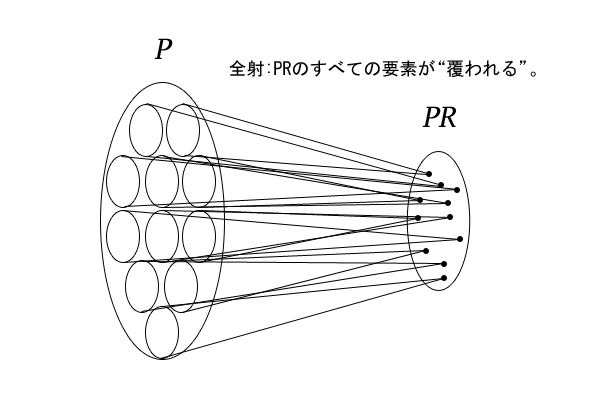
P→PRの写像
図４：$P \rightarrow PR$の写像

集合$PR$の一つの要素に移される集合$P$の要素の数は、後半の$n-r$個の順列の個数に等しいので、つまり、$(n-r)!$個になります。それは、集合$PR$のどの要素についても等しいわけです。したがって、$n$個から$r$個を取り出した順列の集合$PR$の要素数は、$\frac{n!}{(n-r)!}$となります。これを
\[{}_n^{}P_{r}=\frac{n!}{(n-r)!}\]
と書くのでした。

組合せの集合

n個からr個を取り出した組合せ

組合せとは、順列の並び順を無視したものを言います。つまり、$n$個から$r$個を取り出した組合せとは、$n$個から$r$個を取り出した順列において、並び順を入れ替えれば等しくなる順列を同一視したものになります。

集合で考えれば、$n$個から$r$個を取り出した組合せの集合を$CR$とすると、集合$CR$は、集合$PR$の要素において並び順を入れ替えれば等しい要素を同一視したものと言えます。例えば、$\ a_{1}a_{2}a_{3} \cdots a_{r-1}a_{r}$と$a_{1}a_{2}a_{3} \cdots a_{r}a_{r-1}$を一つの要素と考えるわけです。つまり、昇順（小から大の順番）で整列された代表となる要素でそれを表すと、
\[CR=\{\ a_{1}a_{2}a_{3} \cdots a_{r-1}a_{r},\ \ \ a_{1}a_{2}a_{3} \cdots a_{r-1}a_{r+1},\ \ \ \cdots \ \ \ , a_{n-r}a_{n-r+2}a_{n-r+3} \cdots a_{n-1}a_{n}, \ \ \ a_{n-r+1}a_{n-r+2}a_{n-r+3} \cdots a_{n-1}a_{n}\ \}\]
となります。

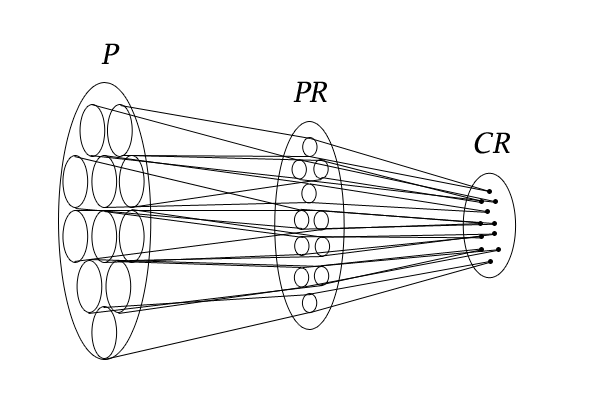
PR→CRの写像
図５：$PR \rightarrow CR$の写像

この同一視の作業を集合の写像として捉えれば、$PR \rightarrow CR$の写像で、集合$PR$の要素から$G$の同一の要素を含む集合$CR$の要素への写像となります。集合$CR$の一つの要素に移される集合$PR$の要素の個数は、$r$個の順列の個数に等しく、それはすべての集合$CR$の要素において同じなので、集合$CR$の要素数は、集合$PR$の要素数を$r!$で割った$\frac{n!}{r!\cdot (n-r)!}$となります。

これを
\[{}_n^{}C_{r}=\frac{n!}{r!\cdot (n-r)!}\]
と書くのでした。

二項定理

二項定理とは$(a+b)^n$の展開式のことです。具体的には、
\[(a+b)^n = {}_n^{}C_{0}a^{n}+{}_{n}^{}C_{1}a^{n-1}b^{1}+{}_{n}^{}C_{2}a^{n-2}b^{2}+\cdots +{}_{n}^{}C_{r}a^{n-r}b^{r}+\cdots +{}_{n}^{}C_{n-1}a^{1}b^{n-1}+{}_{n}^{}C_{n}b^{n} \]
が成り立つことです。

それでは、この二項定理を証明して行きたいと思います。この章では、数学Ⅰ「数と式」で学ぶ整式の加法、乗法における結合法則、分配法則、交換法則を用いるので、ここで復習します。

結合法則：
\[ (a+b)+c =a+(b+c),\ \ (ab)c=a(bc) \]
分配法則：
\[a(b+c) = ab+ac,\ \ (a+b)c=ac+bc\]
交換法則：
\[a+b = b+a,\ \ ab=ba\]
整式の加法、乗法は、上記の３法則を基礎にして変形を行うのでした。
（以上は、概ね高校数学の教科書より引用しました。）

展開された各項の順列

それでは、$(a+b)^n$を展開していきますが、このままだと展開式が少し分かりにくいので、
$a=a_1=a_2= \cdots =a_n$
$b=b_1=b_2= \cdots =b_n$
とおくことで、
\[(a+b)^n = (a_1+b_1)(a_2+b_2) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})\]
と書き直しましょう。

まず、左側から分配法則のみを用いて展開していきます。
\begin{eqnarray}
& & (a_1+b_1)(a_2+b_2) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n}) \\ \\
& = & a_1(a_2+b_2) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})+b_1(a_2+b_2) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})\\ \\
& = & a_1 a_2(a_3+b_3) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})+a_1 b_2(a_3+b_3) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})\\
& + & b_1 a_2(a_3+b_3) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})+b_1 b_2(a_3+b_3) \cdots (a_{n-1}+b_{n-1})(a_{n}+b_{n})\\ \\
& = &\cdots\\ \\
& = & a_1 a_2 \cdots a_{n-1} a_{n} + a_1 a_2 \cdots a_{n-1} b_{n} + \cdots + b_1 b_2 \cdots b_{n-1} a_{n} + \cdots + b_1 b_2 \cdots b_{n-1} b_{n}
\end{eqnarray}

このように、結果として添数が$1, 2, \cdots , n$と昇順に整列され、各添数の位置に$a$又は$b$が表れ、そして、それが互いに少なくとも一つは異なっています。そして、そのようなすべての順列が各項に表れていることが分かります。

ここから交換法則と結合法則を用いて、$a$を因数に含む個数と$b$を因数に含む個数が等しい項を集めれば、二項定理の展開式となります。つまり、$a$を因数に含む個数と$b$を因数に含む個数が等しい項の個数が、二項定理の展開式の各項の係数となるわけです。

添数を消した各項の順列

それでは、$a$を因数に含む個数を$r$個、したがって、$b$を因数に含む個数が$n-r$個である項に着目して、それがいくつあるのかを考えてみたいと思います。この項を積ではなく単純に順列としてみなして、そのような順列を要素に持つ集合を$QR$としておきましょう。例えば、集合$QR$の要素は$a_1 a_2 \cdots a_{r-1} a_{r} b_{r+1} b_{r+2} \cdots b_{n-1} b_{n}$です。

さらに、二項定理の係数にとって大事なのは、$a$を因数に含む個数と$b$を因数に含む個数であって添数は関係がないので、冒頭の等式
$a=a_1=a_2= \cdots =a_n$
$b=b_1=b_2= \cdots =b_n$
で各順列の添数を消した順列を要素とする集合を$QR^{‘}$としておきます。昇順の添数を消しただけなので、$QR$と$QR^{‘}$が一対一対応であることは押さえておきましょう。各添数の位置に$a$又は$b$が互いに少なくとも一つは異なって表れているので、添数を消しても重複が生まれるということはないのです。例えば、集合$QR^{‘}$の要素の一つは$a a \cdots a a b b \cdots b b$です。

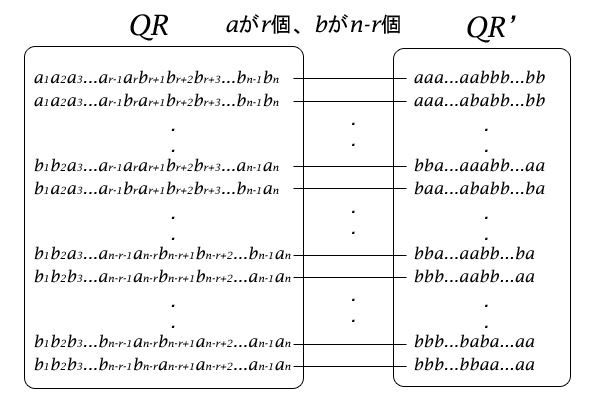
QRとQR'が一対一対応
図６：$QR$と$QR^{‘}$が一対一対応

一般の順列の集合との対応関係

今、先ほどの順列における議論を思い出して、順列の集合$P$とこの$QR^{‘}$の対応関係を考えてみたいと思います。

まず、順列の集合$P$の元となる一般の有限な集合$G=\{a_{1}, a_{2}, a_{3}, \cdots, a_{n-1}, a_{n}\}$について、これは自然数では分かりにくいために便宜的に添数付アルファベットで表したので、別に一対一対応さえ付けばどのようなアルファベットを用いても違いはないのでした。そこで、$G$の先頭$r$個のみを$a$として残し、後半の$n-r$個を$b$に置き換えましょう。つまり、
\[G^{‘}=\{a_{1}, a_{2}, a_{3}, \cdots, a_{r-1}, a_{r}, b_{r+1}, b_{r+2}, b_{r+3}, \cdots, b_{n-1}, b_{n}\}\]
とします。区別のため名称は$G^{‘}$とします。添数を使えばたしかに$a$であろうが$b$であろうが一対一対応が付けられますね。

そして、この$G^{‘}$から順列の集合$P^{‘}$を作っても、元の順列の集合$P$とは、$a$と$b$を交換するだけで一対一対応が保たれているのです。どちらにせよ、したがって集合$P^{‘}$の要素数は$n!$個となります。例えば、集合$P^{‘}$の要素の一つは$a_1 a_2 \cdots a_{r-1} a_{r} b_{r+1} b_{r+2} \cdots b_{n-1} b_{n}$です。

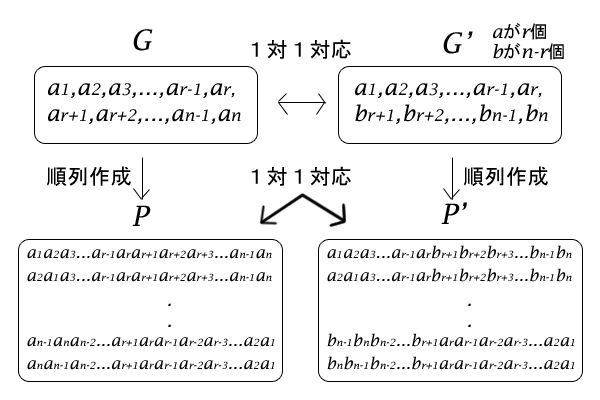
G、P、G'、Pの関係
図７：$G$、$P$、$G^{‘}$、$P^{‘}$の関係

そして、集合$P^{‘}$の要素を一つ取り出して、その添数のみを消してみます。すると、これは集合$QR^{‘}$の要素となっています。例えば、$a_1 a_2 \cdots a_{r-1} a_{r} b_{r+1} b_{r+2} \cdots b_{n-1} b_{n}$の添数を消せば、$a a \cdots a a b b \cdots b b$でたしかにこれは集合$QR^{‘}$の要素です。

この集合$P^{‘}$の要素を一つ取り出して、その添数のみを消す操作は、集合$P^{‘}$のどの要素についても考えられますし、結果は必ず集合$QR^{‘}$のいずれかの要素になるので、集合$P^{‘}$から集合$QR^{‘}$への写像$P^{‘} \rightarrow QR^{‘}$（対応関係）と捉えることができます。くわえて、集合$QR^{‘}$のいずれの要素についても、この写像によって移される元となる要素が集合$P^{‘}$に存在すること（全射）であることも押さえて下さい。

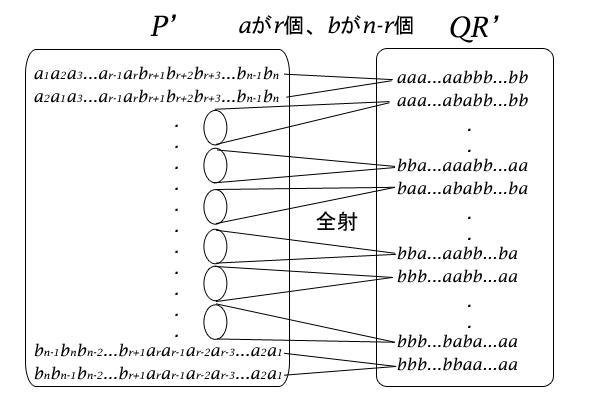
P'とQR'の関係
図８：$P^{‘}$と$QR^{‘}$の関係

では、集合$P^{‘}$と集合$QR^{‘}$は一対一対応かというと、そうではありません。例えば、集合$P^{‘}$の要素である順列$a_1 a_2 a_3 \cdots a_{r-1} a_{r} b_{r+1} b_{r+2} \cdots b_{n-1} b_{n}$と、$a_2 a_1 a_3 \cdots a_{r-1} a_{r} b_{r+1} b_{r+2} \cdots b_{n-1} b_{n}$は、添数を消せばどちらも$a a \cdots a a b b \cdots b b$に対応することになります。つまり、$a$と$b$の位置以外で、添数の順列が異なる要素は集合$QR^{‘}$の同じ要素に対応することになります。

そして、$a$と$b$の位置さえ定まれば、その添数の順列は$a$について$r$個の数の順番の入れ替えなので$r!$個あり、$b$について$n-r$個の数の順番の入れ替えなので$(n-r)!$個あり、この$a$と$b$の添数の順列の個数は、どの$a$と$b$の位置においても同じなのです。

したがって、積の法則から集合$QR^{‘}$の一つの要素に対応する集合$P^{‘}$の要素は、常に$r! \cdot (n-r)!$個あることが分かりました。集合$P^{‘}$の要素数は$n!$個でしたので、集合$QR^{‘}$の要素数は、
\[\frac{n!}{r! \cdot (n-r)!} = {}_n^{}C_{r}\]
であることが言えました。

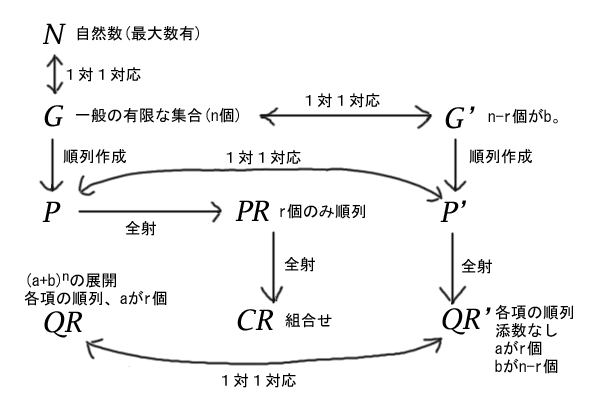
図９：全体図、各集合の定義と関係

さかのぼると、集合$QR^{‘}$は集合$QR$と一対一対応で、集合$QR$は$a$を因数に含む個数を$r$個、$b$を因数に含む個数が$n-r$個である項の集合だったので、$a$を因数に含む個数を$r$個、$b$を因数に含む個数が$n-r$個の個数は${}_n^{}C_{r}$個であり、交換法則と結合法則を用いてこれらの項を集めれば、$a^{r}b^{n-r}$の係数が${}_n^{}C_{r}$となります。

冒頭の式における$a^{n-r}b^{r}$と指数が逆になっていますが、$n-r$を$r^{‘}$、したがって、$r$を$n-r^{‘}$と置き換えても冒頭の展開式は成り立ちます。つまり、
\[(a+b)^n = {}_n^{}C_{n}a^{n}+{}_{n}^{}C_{n-1}a^{n-1}b^{1}+{}_{n}^{}C_{n-2}a^{n-2}b^{2}+\cdots +{}_{n}^{}C_{r^{‘}}a^{n-r^{‘}}b^{r^{‘}}+\cdots +{}_{n}^{}C_{1}a^{1}b^{n-1}+{}_{n}^{}C_{0}b^{n} \]
も同じことなので、これで二項定理を証明することができました。

さらに付け加えると、前章で組合せの集合として以下のような集合$CR$を考えましたが、

\[CR=\{\ a_{1}a_{2}a_{3} \cdots a_{r-1}a_{r},\ \ \ a_{1}a_{2}a_{3} \cdots a_{r-1}a_{r+1},\ \ \ \cdots \ \ \ , a_{n-r}a_{n-r+2}a_{n-r+3} \cdots a_{n-1}a_{n}, \ \ \ a_{n-r+1}a_{n-r+2}a_{n-r+3} \cdots a_{n-1}a_{n}\ \}\]

上記の添数が抜けた箇所に順序通りの添数が付いた$b$を挿入すれば、集合$QR$の要素となり、逆に、集合$QR$の要素から添数付の$b$を削除すれば、集合$CR$の要素となり、この操作により互いの要素は一対一に対応していることが分かります。また、集合$QR^{‘}$は集合$QR$と一対一対応でしたので、結局、集合$CR$と集合$QR^{‘}$は一対一対応であり、集合$QR^{‘}$はこのページの定義による$n$個から$r$を取り出した組合せの集合$CR$と同一視することができるということが分かります。

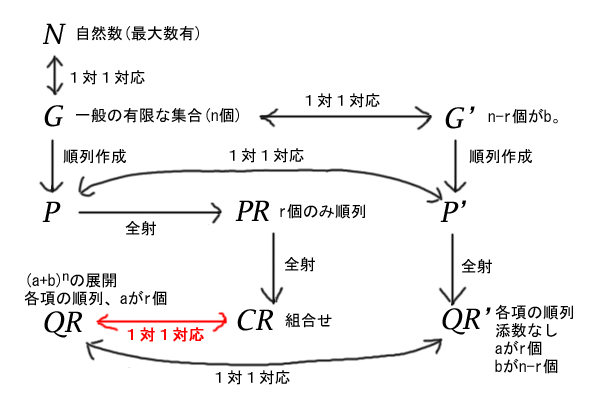
集合CR、QR、QR'の関係
図１０：集合$CR$、$QR$、$QR^{‘}$の関係

教科書の証明との違い

高校数学の教科書では、組合せを用いて二項定理を証明しています。上記の証明法は、手数は格段に多いですが、この証明法を読んでから高校数学の教科書を読み返すと、高校数学の教科書の記述は少し直観的であったことを感じて頂けるのではないかと思います。

上記の記述は、かなり詳細な解説を含んで書いたために長くなりましたが、本当に必要な記述はもっと少なくて済みます。どんな数学分野でも同じですが、直観的な推論を一つ一つの原理にまで分割（分解）し、その一つ一つの原理に基づいて推論を進めることによって、推論の回数は増えますがより正確に物事を考えることができ、より複雑な命題へと推論を進めて行くことができるようになります。

そのことを実感としてこのページでも掴んで頂けるのではないかと思います。具体的には、集合とその対応関係、自然数による有限と無限の基礎付け、がこのページの原理になっています。大学範囲では、より正確な議論で学ぶことができます。何のために集合を用いているのか、メリットそしてデメリットも理解できるようになると良いのではないかと思います。

パスカルの三角形

パスカルの三角形とは、以下のような数の配列です。
　　　　　１　１
　　　　１　２　１
　　　１　３　３　１
　　１　４　６　４　１
　１　５　10　10　５　１
１　６　15　20　15　６　１
$\cdots$
一段づつ隣接する二つの数を足した和が、その二つの数の下段の間に書かれていきます。なぜこのような配列が重要かというと、各$n$段目の数列が$(a+b)^{n}$の各項の係数になっているからです。つまり、前節での考察によると、組合せ${}_n^{}C_{r}$の数列：
\[{}_n^{}C_{0},\ {}_n^{}C_{1},\ {}_n^{}C_{2},\ \cdots,\ {}_n^{}C_{r}, \cdots,\ {}_n^{}C_{n-2},\ {}_n^{}C_{n-1},\ {}_n^{}C_{n}\]
がきれいに$n$段目に並んでいることになります。

二項定理との対応

高校数学の教科書では、この事実を$(a+b)^{n}$の展開式とパスカルの三角形を直接に対応付けて、それから$(a+b)^{n}$の二項定理（展開式の係数が組合せ${}_n^{}C_{r}$であること）を学ぶことで、パスカルの三角形と組合せ${}_n^{}C_{r}$の数列の一致を確認します。つまり、$(a+b)^{n}$の展開式を軸として考えるわけです。

ここでの説明も基本的には同じことなのですが、もう少し明確な対応関係を確認したいと思います。まず、その復習から入ると、順列の集合$P$の元となる一般の有限な集合$G=\{a_{1}, a_{2}, a_{3}, \cdots, a_{n-1}, a_{n}\}$について、これは自然数では分かりにくいために便宜的に添数付アルファベットで表したので、別に一対一対応さえ付けばどのようなアルファベットを用いても違いはないのでした。そこで、$G$の先頭$r$個のみを$a$として残し、後半の$n-r$個を$b$に置き換えましょう。つまり、
\[G^{‘}=\{a_{1}, a_{2}, a_{3}, \cdots, a_{r-1}, a_{r}, b_{r+1}, b_{r+2}, b_{r+3}, \cdots, b_{n-1}, b_{n}\}\]
とします。区別のため名称は$G^{‘}$とします。添数を使えばたしかに$a$であろうが$b$であろうが一対一対応が付けられますね。

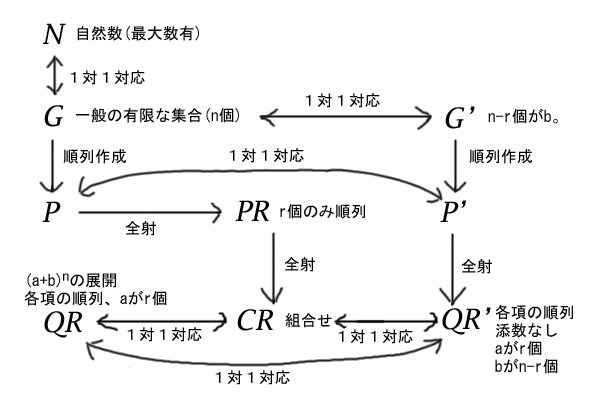
図１１：全体の復習

さて、そのパスカルの三角形と組合せの明確な対応関係ですが、せっかく一般の有限な集合$G$を考えているので、集合$G$のアルファベットを代えただけの集合$G^{‘}$、集合$G^{‘}$から導いた順列の集合$P^{‘}$、さらに集合$P^{‘}$からその順列の添数を消して導いた集合とも言える集合$QR^{‘}$（これが組合せの集合$CR$と一対一対応）を使って、集合$QR^{‘}$を軸としてパスカルの三角形と組合せ${}_n^{}C_{r}$の数列との対応関係を解説したいと思います。

すでに前章の二項定理で、集合$QR^{‘}$の要素数が組合せ${}_n^{}C_{r}$で、組合せの集合$CR$と一対一対応であることも示しました。したがって、集合$QR^{‘}$の要素数と、パスカルの三角形の$n$段目、先頭を$0$列として左から$r$列目にある数が、等しいことを示せば良いことになります。

集合$QR^{‘}$の要素は、$n$個のうち$r$個が$a$で$n-r$個が$b$の添数の消された順列、例えば$a a \cdots a a b b \cdots b b$でした。このような$a$と$b$の個数が等しいすべての順列が、集合$QR^{‘}$の要素ということになります。

それでは、集合$QR^{‘}$の中身を見てみると、先頭が$a$か$b$かで集合$QR^{‘}$の要素は、二種類に区別することができることが分かります。そこで、先頭が$a$の順列を要素に持つ集合$QR^{‘}$の部分集合を$QR^{‘}A$、先頭が$b$の順列を要素に持つ集合$QR^{‘}$の部分集合を$QR^{‘}B$とすると、集合$QR^{‘}$は、部分集合$QR^{‘}A$と部分集合$QR^{‘}B$とに排反に分割することができました。

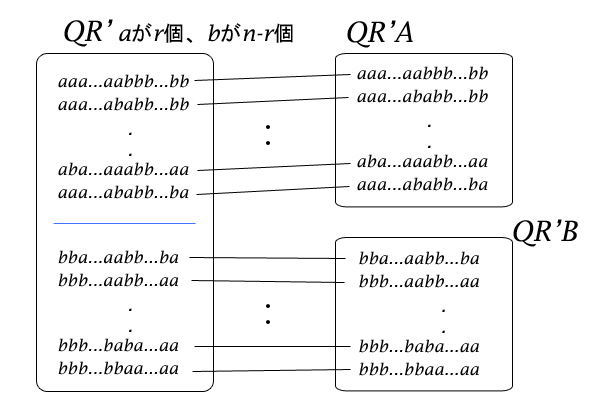
集合QR'、QR'A、QR'Bの関係
図１２：集合$QR^{‘}$、$QR^{‘}A$、$QR^{‘}B$の関係

次に、集合$QR^{‘}A$の中身を見てみると、集合$QR^{‘}A$のすべての要素は先頭が$a$です。そこで、その先頭の$a$を隠してみます。そうすると、その各要素は、$n-1$個のうち$r-1$個が$a$で$n-r$個が$b$の添数の消された順列であることが分かります。そこで、この$n-1$個のうち$r-1$個が$a$で$n-r$個が$b$の添数の消された順列を要素に持つ集合を$n-1Qr-1^{‘}$とすると、集合$n-1Qr-1^{‘}$の要素の順列の先頭に$a$を付ければ、集合$QR^{‘}A$の要素になることが分かります。したがって、集合$QR^{‘}A$と集合$n-1Qr-1^{‘}$の違いは、先頭に$a$があるかないかだけで、両者は一対一対応しています。

同様に、集合$QR^{‘}B$の中身を見てみると、集合$QR^{‘}B$のすべての要素は先頭が$b$です。そこで、その先頭の$b$を隠してみます。そうすると、その各要素は、$n-1$個のうち$r$個が$a$で$n-r-1$個が$b$の添数の消された順列であることが分かります。そこで、この$n-1$個のうち$r$個が$a$で$n-r-1$個が$b$の添数の消された順列を要素に持つ集合を$n-1Qr^{‘}$とすると、集合$n-1Qr^{‘}$の要素の順列の先頭に$b$を付ければ、集合$QR^{‘}B$の要素になることが分かります。したがって、集合$Qr^{‘}B$と集合$n-1Qr^{‘}$の違いは、先頭に$b$があるかないかだけで、両者は一対一対応しています。

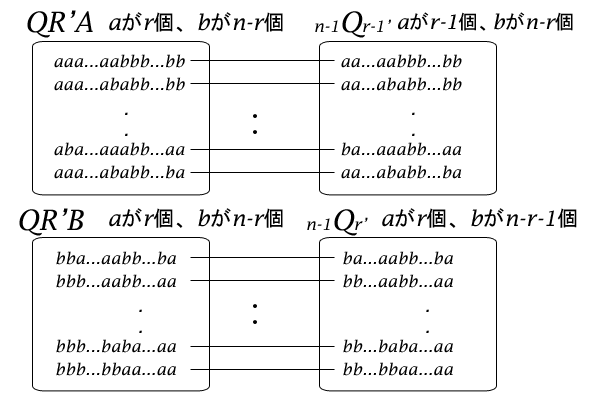
集合QR'Aとn-1Qr-1'、集合QR'Bとn-1Qr'の各関係
図１３：集合$QR^{‘}A$と$n-1Qr-1^{‘}$、集合$QR^{‘}B$と$n-1Qr^{‘}$の各関係

したがって、集合$QR^{‘}$の排反な部分集合$QR^{‘}A$と部分集合$QR^{‘}B$は、それぞれ集合$n-1Qr-1^{‘}$と集合$n-1Qr^{‘}$と一対一対応していることが分かりました。この操作は、同様に集合$n-1Qr-1^{‘}$と集合$n-1Qr^{‘}$についても適用して、集合$n-1Qr-1^{‘}$からは集合$n-2Qr-1^{‘}$と集合$n-2Qr-2^{‘}$を、集合$n-1Qr^{‘}$からは集合$n-2Qr^{‘}$と集合$n-2Qr-1^{‘}$を導き出すことができます。

そして、この操作を繰り返すと、操作ごとに必ず$Q$の左側の要素数（総数）が一つづつ下がっていくことが分かります。また、$Q$の左側の要素数（総数）と右側の$a$の個数が等しくなった場合、つまり、$xQx^{‘}$で$a$が$x$個並ぶ順列$aa \cdots aa$が一つのみの要素である場合でもこの操作は、$xQx^{‘}$から$x-1Qx-1^{‘}$のみを導き出す操作として考えられ、あるいは、$Q$の右側の$a$の個数が$0$なった場合、つまり、$xQ0^{‘}$で$b$が$x$個並ぶ順列$bb \cdots bb$が一つのみの要素である場合でもこの操作は、$xQ0^{‘}$から$x-1Q0^{‘}$のみを導き出す操作として考えられます。

したがって、この操作を最後まで繰り返せば、必ず$1Q1^{‘}$か$1Q0^{‘}$に行き着くことになります。$1Q1^{‘}$は順列$a$のみが要素の集合で、$1Q0^{‘}$は順列$b$のみが要素の集合です。これ以上は先頭文字を除くという操作ができないと考えましょう。

そして最後のポイントとして、隣接している集合$xQy-1^{‘}$と集合$xQy^{‘}$からは、同じ集合$x-1Qy-1^{‘}$が共に導き出されていたことに注意してください。したがって、同じ集合$x-1Qy-1^{‘}$を複数考える必要はなく、一つだけ書くようにしてこの操作の繰り返しを図示すると下記のようになります。

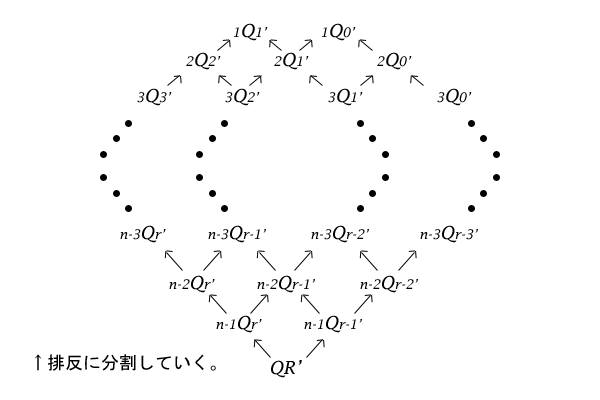
$集合QR'\)の分割$
図１４：集合$QR^{‘}$の分割

この操作を逆に導き出された$1Q1^{‘}$か$1Q0^{‘}$から辿って行けば集合$QR^{‘}$に行き着くことになります。そのとき、逆の操作は、それぞれ集合$x-1Qy^{‘}$と集合$x-1Qy-1^{‘}$がその分割前の集合$xQy^{‘}$の排反に分割された部分集合と１対１対応しているのでした。したがって、その集合$xQy^{‘}$の要素数も集合$x-1Qy^{‘}$と集合$x-1Qy-1^{‘}$の要素数の和になることが分かります。

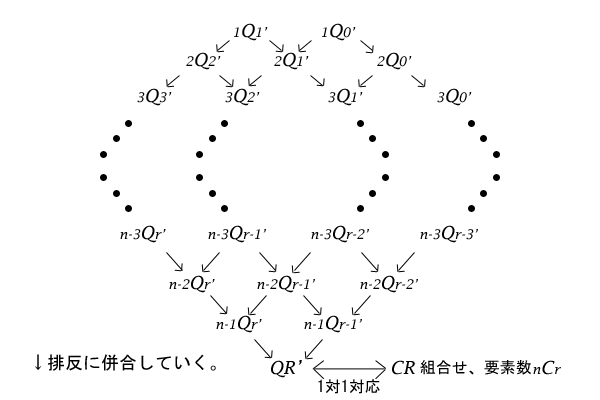
集合QR'への併合と集合QR'、集合CR、要素数nCr
図１５：集合$QR’$への併合と集合$QR^{‘}$、集合$CR$、要素数${}_n^{}C_{r}$

集合$1Q1^{‘}$の要素数は$1$、集合$1Q0^{‘}$の要素数も$1$なので、パスカルの三角形の作成方法である「一段づつ隣接する二つの数を足した和を、その二つの数の下段の間に書く」という操作と一致していることが分かります。したがって、集合$QR^{‘}$の要素数と、パスカルの三角形の$n$段目、先頭を$0$列として左から$r$列目にある数が等しいことが示せました。

これと、前章の二項定理で示された、集合$QR^{‘}$の要素数が組合せ${}_n^{}C_{r}$で、組合せの集合$CR$と一対一対応であることも併せれば、集合$QR^{‘}$を介して、パスカルの三角形の$n$段目$r$列目にある数は、組合せ${}_n^{}C_{r}$であることも分かりました。

実際には、パスカルの三角形を数としての組合せ${}_n^{}C_{r}$で表せることを示しただけではなく、このページにおける組合せの集合$CR$によって、集合と写像の関係としてパスカルの三角形を表わすことができたことにも注意してみてください。

平面座標の道順との対応

平面座標を通常は$xy$座標として考えますが、ここではアルファベットを合わせるため$ab$座標として考えましょう。平面座標の座標がすべて整数となっている点を格子点と呼びます。また、$a$軸や$b$軸に平行で格子点を通る直線を格子と呼びましょう。簡単のため、平面座標$ab$の$a$軸も$b$軸も$0$を含んだ正の場合のみを考えることとします。

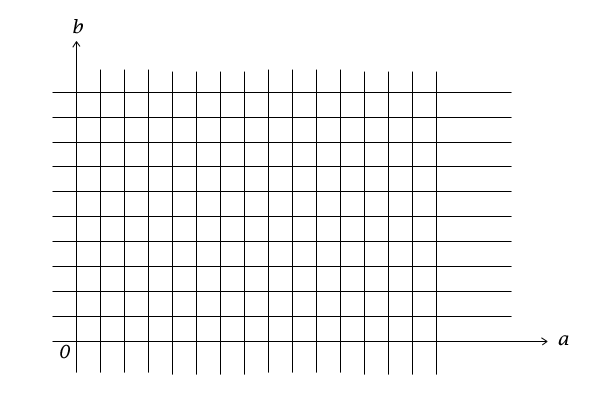
ab平面の正の格子点
図１６：$ab$平面の正の格子点

今、平面座標$ab$内のある格子点$A$について、平面座標$ab$の中心の点$O=(0,0)$から正の方向のみに格子のみを通って格子点$A$に至る道順を、格子点$A$への道順と呼ぶことにします。「正の方向のみ」というのは逆戻りはしないということです。

格子点$A$への道順は、中心の点$O=(0,0)$から出発して、格子点のみで分岐の可能性があり、格子点においてはいつも$a$軸方向か$b$軸方向への二者択一が生じます。したがって、その選択を点$O=(0,0)$から順番に$aabbababb\cdots$と書き表すことができます。例えば、格子点$A=(3,2)$ならば、$ababa$が一つの道順を表すことになります。

ここで、格子点$A$への道順を$aabbababb\cdots$のように明確に表すことができたので、格子点$A$へのすべての道順を要素とする集合を$DA$としましょう。格子点$A$の座標を$(c,d)$とすると、集合$DA$の各道順において$a$は$c$個、$b$は$d$個あることは変わりません。当然、$c+d$も一定の数です。

そうすると、これは今まで見てきた、$n$個のうち$r$個が$a$で$n-r$個が$b$の添数の消された順列の集合$QR^{‘}$において、$r=c$、$n-r=d$、$n=c+d$と置いたものと、まったく同じであることが分かります。

集合$QR^{‘}$は組合せの集合$CR$と一対一対応でその要素数は${}_n^{}C_{r}$個なのでした。したがって、集合$DA$の要素数も${}_n^{}C_{r}$個、つまり、${}_{c+d}^{}C_{c}$個になることが分かりました。

ここで面白いのは、一般の有限な集合$G^{‘}$から導いた順列の集合$P^{‘}$、さらに集合$P^{‘}$からその順列の添数を消して導いた集合とも言える集合$QR^{‘}$を考えると、集合$QR^{‘}$を軸として$(a+b)^{n}$の展開式の各項と平面座標の格子点の道順が一対一対応しうる関係にあるということです。

したがって、$(a+b)^{n}$の展開式の各項で成り立つ事柄と、平面座標の格子点の道順で成り立つ事柄は、共通する集合$QR^{‘}$で成り立つ事柄に関してはどちらでも成り立つ、つまり、大げさに言えば各事柄の持つ法則を互いに保存すると言えます。このように思わぬところに新しい関係を見出すことも数学の醍醐味です。

多項定理

高校数学の教科書では、二項定理の後に研究において$(a+b+c)^{n}$の展開式を学習しています。二項定理が$(a+b)^{n}$の$a$と$b$の二項の展開式であるのに対して、$(a+b+c)^{n}$の展開式は、$a$と$b$と$c$の三項の展開式になっています。このように、$n$べき乗の中身が三項以上の和になっている場合の展開式を多項定理と呼びます。

教科書では三項のみを扱っていますが、$m$項についても原理はまったく変わらず、つまり、
\[(a_{1} + a_{2} + \cdots + a_{m-1} + a_{m})^{n}\]
の展開式の各項
\[a_{1}^{p_1}a_{2}^{p_2} \cdots a_{m-1}^{p_{m-1}}a_{m}^{p_{m}}\]
ただし、$0 \leq p_1,p_2, \cdots, p_{m-1}, p_{m} \leq n$　かつ　$p_1 + p_2 + \cdots + p_{m-1} + p_{m} = n$
の係数は、
\[\frac{n!}{p_1!p_2! \cdots p_{m-1}!p_{m}!}\]
となります。

教科書では、この証明を二項定理と同様に少し直観的に組合せを用いて行っています。それでも慣れてしまえば二項定理の証明とそれほどギャップを感じることはないと思いますが、このページで行った二項定理の証明方法であれば、二項を多項に置き換えるだけで、ほぼ同じ論法で証明を終えることができます。

二項定理の証明を振り返ると、まず、一般の有限な集合$G$の先頭$r$個のみを$a$として残し、
後半の$n-r$個を$b$に置き換えた集合$G^{‘}$、
\[G^{‘}=\{a_{1}, a_{2}, a_{3}, \cdots, a_{r-1}, a_{r}, b_{r+1}, b_{r+2}, b_{r+3}, \cdots, b_{n-1}, b_{n}\}\]
を考えました。そして、集合$G^{‘}$から順列の集合$P^{‘}$を考え、集合$P^{‘}$の添数を消した集合が、$(a+b)^{n}$を分配法則のみで展開し、未だ交換法則や結合法則でまとめずに、その上で$a$が$r$個、$b$が$n-r$個ある各項を単純に順列とみなした集合$QR^{‘}$を考え、集合$QR^{‘}$の要素数として、
\[\frac{n!}{r! \cdot (n-r)!}\]
と導きました。したがって、この集合$QR^{‘}$の要素数こそが、交換法則や結合法則でまとめた$a$が$r$個、$b$が$n-r$個ある項の係数になるのでした。

多項定理の場合は、初めの一般の有限な集合$G$の先頭$p_1$個を$a_1$とし、次の$p_2$個を$a_2$とし、引き続き、最後の$p_m$個を$a_m$と置き換えた集合$G^{‘}$を考えれば、あとは同様に考えれば済みます。二項定理と比較すると、$a$が$a_1$に、$b$が$a_2$に対応しているわけです。

具体的には、集合$G^{‘}$は添数が重複して少しややこしいですが、前がアルファベットの種類としての添数、後が要素としての元の添数と考えて、
\begin{eqnarray}
G^{‘} & = & \{a_{(1,1)},\ a_{(1,2)},\ a_{(1,3)},\ \cdots,\ a_{(1,p_{1}-1)},\ a_{(1,p_1)}, \\
&& \{a_{(2,p_1+1)},\ a_{(2,p_1+2)},\ a_{(2,p_1+3)},\ \cdots,\ a_{(2,p_{2}-1)},\ a_{(2,p_1+p_2)}, \\
&& \cdots \\
&& \{a_{(m,n-p_m+1)},\ a_{(m,n-p_m+2)},\ a_{(m,n-p_m+3)},\ \cdots,\ a_{(m,n-1)},\ a_{(m,n)}\}
\end{eqnarray}
となります。

そして、集合$G^{‘}$から後の添数を用いて順列の集合$P^{‘}$を考え、集合$P^{‘}$の後の添数を消した集合が、$(a_{1} + a_{2} + \cdots + a_{m-1} + a_{m})^{n}$を分配法則のみで展開し、未だ交換法則や結合法則でまとめていない各項を単純に順列とみなした集合$QR^{‘}$となります（本来は、集合$Qp_1p_2\cdots p_{m-1}^{‘}$のように書いた方が対応関係が分かりやすいかもしれませんが、煩雑なのでやめます）。

ここで、集合$P^{‘}$の要素数は、やはり$n!$個です。さらに、集合$QR^{‘}$の要素を一つ取り出せば、いずれの要素であっても、消された「後の添数」による順列の個数だけ集合$P^{‘}$の要素と対応します。消された「後の添数」に表れる順列の個数は、積の法則より$p_1!p_2! \cdots p_{m-1}!p_{m}!$個となります。したがって、集合$QR^{‘}$の要素数、つまり、係数は、
\[\frac{n!}{p_1!p_2! \cdots p_{m-1}!p_{m}!}\]
と導くことができました。

ここで念のため注意しておくと、集合$QR^{‘}$というのは$m$個の異なる種類の総数$n$個でそれぞれ$p_1,p_2, \cdots p_{m-1},p_{m}$個あるものを並べる順列、いわゆる重複順列といいます。つまり、$m=2$の２種類のときには、重複順列の集合$QR^{‘}$と組合せの集合$CR$が一対一対応であるということをこのページでは用いてきました。

発展：多項定理と道順とパスカルの三角形

多項定理と多次元座標の格子点の道順

ここまで、一般の有限な集合$G$、集合$G$のアルファベットを代えただけの集合$G^{‘}$、集合$G^{‘}$から導いた順列の集合$P^{‘}$、さらに集合$P^{‘}$からその順列の添数を消して導いた２種類の重複順列の集合とも言える集合$QR^{‘}$（組合せの集合$CR$と一対一対応）を軸として、集合$QR^{‘}$の要素数と、組合せ${}_n^{}C_{r}$、二項係数、パスカルの三角形、平面座標の格子点の道順が対応していることを示しました。

そして、多項定理では、
\[G^{‘}=\{a_{1}, a_{2}, a_{3}, \cdots, a_{r-1}, a_{r}, b_{r+1}, b_{r+2}, b_{r+3}, \cdots, b_{n-1}, b_{n}\}\]
を、
\begin{eqnarray}
G^{‘} & = & \{a_{(1,1)},\ a_{(1,2)},\ a_{(1,3)},\ \cdots,\ a_{(1,p_{1}-1)},\ a_{(1,p_1)}, \\
&& \{a_{(2,p_1+1)},\ a_{(2,p_1+2)},\ a_{(2,p_1+3)},\ \cdots,\ a_{(2,p_{2}-1)},\ a_{(2,p_1+p_2)}, \\
&& \cdots \\
&& \{a_{(m,n-p_m+1)},\ a_{(m,n-p_m+2)},\ a_{(m,n-p_m+3)},\ \cdots,\ a_{(m,n-1)},\ a_{(m,n)}\}
\end{eqnarray}
と置き換えて、あとは二項定理と同様に考えることで、集合$QR^{‘}$の要素数と、$\frac{n!}{p_1!p_2! \cdots p_{m-1}!p_{m}!}$、多項係数が対応していることを示しました。それでは、この場合の残りの「パスカルの三角形、平面座標の格子点の道順」とは何でしょうか？

それは、初めに平面座標の格子点の道順の考え方の２次元を多次元に置き換えて考えれば分かりやすいと思います。つまり、$m$次元では、各格子点において進むことのできる次の格子点は$m$個あるわけで、これは集合$QR^{‘}$の要素が$m$種類のアルファベット（前の添数）あることと対応付けることができます。たしかに、集合$QR^{‘}$のある一つの要素は、$m$種類のアルファベット（前の添数）が進む方向を表していると考えれば、その$m$次元における距離$n$のある一つの格子点への道順に対応させられます。

多次元に拡張されたパスカルの三角形

$m$次元の距離$n$の任意の格子点は、その格子点の一つ前にある距離$n-1$の格子点からしか入って来れないので、その道順は、一つ前にある距離$n-1$のすべての格子点の道順の総和となります。これは、２次元で言えば、パスカルの三角形の数の配列の作り方そのものです。したがって、パスカルの三角形の数の配列の作り方を多次元に拡張すると、多次元の格子点の道順になる、それはつまり、集合$QR^{‘}$の要素数と対応しているということが分かります。

というのは、パスカルの三角形では、２種類の重複順列の集合$QR^{‘}$と写像でパスカルの三角形を置き換えることができましたが、２種類に分割・併合するのではなく、$m$種類に分割・併合を行う操作を考えれば、多次元に拡張されたパスカルの三角形も同様に$m$種類の重複順列の集合$QR^{‘}$と写像で置き換えて考えることができます。

自然数のべき乗と多次元座標の格子点の道順

そうすると、例えば、多項定理の式
\[(a_{1} + a_{2} + \cdots + a_{m-1} + a_{m})^{n}\]
に
\[a_{1} = a_{2} = \cdots = a_{m-1} = a_{m} = 1\]
と、すべての変数に$1$を代入すると、すべての以下のような多項係数
\[\frac{n!}{p_1!p_2! \cdots p_{m-1}!p_{m}!}\]
ただし、$0 \leq p_1,p_2, \cdots, p_{m-1}, p_{m} \leq n$　かつ　$p_1 + p_2 + \cdots + p_{m-1} + p_{m} = n$
の総和を取ると、
\[ m^{n}= (a_{1} + a_{2} + \cdots + a_{m-1} + a_{m})^{n} = \sum \frac{n!}{p_1!p_2! \cdots p_{m-1}!p_{m}!}\]
となります。
そうすると、ここから$m^{n}$という自然数は、$m$次元の距離$n$のすべての格子点への道順の総和であることが分かります。

このように、よく数式で用いる自然数のべき乗$m^{n}$であっても幾何的な意味を帯びるということは、初めて解説を知った時にはとても不思議な気持ちになったのを思い出します。ただし、幾何的な意味といっても多次元を「目に見える形」に捉えられるわけではないので、ここでは多次元座標として、という意味合いです。

もちろん、自然数のべき乗$m^{n}$のもっと単純な幾何的な意味としては、$n$次元の各辺に$m$個の格子点のある正方形や立方体のような図形が含む格子点の総数としても捉えられます。面白いのは、上記の道順とは、次元と長さ（距離や辺）が逆になっていることです。どちらも$m^{n}$個あるのですが、前者は「$m$次元の距離$n$のすべての格子点への道順の総和」、後者は「$n$次元の各辺に$m$個の格子点のある正方形や立方体のような図形が含む格子点の総数」というわけです。

フェルマー・ワイルズの定理と格子点と道順、と数学の面白さ

これを例えば、有名なフェルマー・ワイルズの定理「$n\geq 3$のとき、$x^n+y^n=z^n$の$(x,y,z)$に自然数解がない」に当てはめると、少し煩雑ですが、前者は「$z$次元の距離$n$のすべての格子点への道順の総和を、二つの$x$次元の距離$n$のすべての格子点への道順の総和と$y$次元の距離$n$のすべての格子点への道順の総和に分けることはできない」、後者は「$n$次元の各辺に$z$個の格子点のある正方形や立方体のような図形が含む格子点の総数を、二つの$n$次元の各辺に$x$個の格子点のある正方形や立方体のような図形が含む格子点の総数と$n$次元の各辺に$y$個の格子点のある正方形や立方体のような図形が含む格子点の総数に分けることができない」と言い換えることができます。

$n = 2$ならば$x^2+y^2=z^2$で、これはピタゴラスの定理なので、例えば有名な$(3,4,5)$や$(9,12,15)$など無数にあります。なぜ$n\geq 3$になると、途端にできなくなるのか、、。とても不思議ですね。こんなところから幾ばくかの数学者は数学に興味を覚えて、勉学に勤しんできたのではないかと思います。何しろ、３００年程前に、フェルマーが解けたけれど余白がないというメモを残し、徐々に研究が進んで３００年程あとの現代になってやっとワイルズ教授が完全な証明に成功したという長い物語の魅力もあります。こういう伝説的な逸話も数学には古代から数多とあって、素直に楽しめる人にとってはとても楽しい、子供の夢想のような面白さがあります。

少し、あるいは、さらに数学に興味を持って頂けましたでしょうか。フェルマー・ワイルズの定理の証明は、難しくて私には分かりませんが、用いられている理論の細部まで理解している数学者はそれほど多くはないという、それほど難しい証明とのことです。

【以下、追記】
この記事を書いていた頃にコロナ禍が深まり変則的なタイムスケジュールの中、少し時間を取ることができてフェルマー・ワイルズの定理を一から考えてみることができました。結果を論文にまとめ、結局、取り組み始めてから１年半程はかかりましたが論文誌に掲載して頂くこともできました。論文の内容自体は数学科の学部生であればだいたい理解できるものと思います。興味のある方は、将来でもご覧になってみて下さい。論文はこちら⇒「主に組合せ論によって導かれたフェルマー・ワイルズの定理の簡単な条件（原文英語）」です。著作権を掲載誌に譲渡してしまっているので、残念ながら有料リンクをご紹介するしかないのですが、大学によっては図書館に置かれているところもあります。
【以上、追記】

数学で身に付く重要な考え方～柔軟性、枠組み変化、真理探究～

数学では、一見、２次、３次、、、とどこまでも同じような性質を持っていそうな対象が、少し次数が増えるだけでまったく異なる性質を持つようになる場合がたくさんあります。例えば、高校数学に最も近いのは、方程式の解の公式かと思います。２次方程式の解の公式は、高校数学でも習いますね。３次方程式の解の公式と４次方程式の解の公式もありますが、とても複雑なので高校数学では習いません。そして、５次方程式の解の公式になると、そのような公式は作れないということが証明されます。

１、２次だと単純、３次くらいからとっても複雑になる、複雑になると自然数、整数、有理数、無理数、複素数と考える必要のある範囲が広がったり、当たり前の手法や考え方が通じなくなったりする、こんな着眼点も数学の興味深い視点です。

そして、これは数学だけではなく、何事を学ぶ際でも、仕事を行う際でも、このような視点に慣れることは大切なことです。例えば、物理でも地球の上ではユークリッド幾何が通用しますが、宇宙的規模になれば空間は歪みますし、極小に目を移せば確率的にしか物質の位置を捉えることができなくなります。ビジネスでもスモール・ビッグ、ローカル・グローバル、IT革命前後、AI革命前後、コロナ前後などでは、基本となる手法や考え方に大きな違いが生まれ、柔軟に考え方の枠組みを変更しなければならない事象がたくさん起こります。

このように、扱う事象の変化に伴って生じる考え方の枠組み変化にどう対処すべきか、数学で経験を積んでおくことでその対処法を身に付けることができると思います。つまり、環境や状況の新規性に驚いて拒絶するのではなく、これまでの考え方の枠組みのどこが正しいのか正しくないのか、それだけを謙虚に問い直せるか、が新たな環境や状況に対応できるかの大きな分岐点になると感じます。学問においては、この姿勢を真理の探究と表現したりします。

数学を通して学ぶことのできる事柄は多いのですが、特に、考え方の枠組みを変えられる柔軟性を持つこと、多面的に物事を見る姿勢が身に付くこと、そして、それを正しいのか正しくないのかというある程度の明確な基準や結論を意識して判断しょうとする姿勢を身に付けられること、つまり、真理を探究する姿勢を身に付けられること、が数学を学んでいて最も価値のあることだろうと思います。

日本の学校では、小学生、中学生くらいからこのページで説明されている組合せと道順の関係などを学んできたと思います。高校数学の教科書をただ流し読みして、なんだ簡単、あんまり小学生、中学生で習ったことと変わらないじゃん、一年間で読み終わったし、受験問題もそれなりに解けるよ、とか早合点をすると、この分野、さらには数学や科学の本当の面白さ、本当の実力には繋がらないかもしれません。

社会に出ても別に数学は使わなかったし、勉強しても意味はなかったという結論に至る人は多くいます。なぜなら、数学を勉強したつもりで、それほど勉強していないからです。さらに、それよりも大きな問題は、たくさん勉強していても勉強している内容が悪いからです。前者も後者も個人でどうこうできる問題とは限りません。ただ結局、勉強していないもの、身に付いていない考え方、を使うことができないことだけは確かなのです。私もそうでしたし、今でも多いに自分の不勉強を痛感しています。

ただ、このページのようなことまで考えられるようになると、一歩、高校生らしい、というか高校生$+\alpha$に踏み込めたと言えるのかもしれません。

余談ですが実際、少なくとも経済に関しては、学術の発展していない国と学術の発展している国を比べれば、ほぼ「学術の発展している国＝豊かな国」であることが分かると思います。経済主体としての側面が大きな営利企業についても、規模が大きくなればなるほど「学術のある企業」＝「利益の大きな企業」でほぼ間違いありません。ただ、経済だけがすべてではまったくありませんが、。

自然数と格子点の興味深い関係

ここまでで、自然数、順列、組合せ、二項定理、多項定理、べき乗、パスカルの三角形、格子点、道順などには、とても密接な対応関係があることを見てきました。多くの数学の分野の交差点のような様相を呈していますが、これらは概ね組合せ論、グラフ理論という分野で研究されている内容ではないかと思います。私は、残念ながら詳しくありませんが、興味のある方は大学で勉強してみて下さい。

最後に、さらにいくつかこれらの内容に関係する美しい事実を紹介して、このページを終わりたいと思います。以下の内容は、組合せ理論の中でも三角数と接点を持った分野と言えるだろうと思います。三角数はピタゴラスの時代より研究されており、組合せとの関係は１３世紀にペルシャの数学者アル・ファリシによって初めて一般的な指摘を受けたようです。興味のある方は、「組合せ論」「三角数」などでウィキペデイアなども見て下さい。

組合せ、つまり、二項係数の${}_{n} \mathrm{C} _r$の$r$と$n-r$は、多項定理から分かるように、交換可能な対称性を持っているので、$n=x+y$と置き直すと、${}_{x+y} \mathrm{C} _x = {}_{x+y} \mathrm{C} _y$と書け、さらに、パスカルの三角形が$1$の和で構成されていることをよく観察すると、

$${}_{x+y} \mathrm{C} _x\,=\,\sum_{k_1=0}^x(\sum_{k_2=0}^{k_1}(\,\cdot\cdot\cdot\sum_{k_{y-1}=0}^{k_{y-2}}(\sum_{k_y=0}^{k_{y-1}}(1))\,\cdot\!\cdot\cdot\,))$$

という公式を導くことができます。

そして、この公式を格子点として解釈すると、${}_{x+y} \mathrm{C} _x$は、$x$次元座標の原点から距離$y$までの格子点の総数であることが分かります。そうすると、$x, y$は交換可能なので、$x$次元座標の原点から距離$y$までの格子点の総数と$y$次元座標の原点から距離$x$までの格子点の総数が等しいことも分かります。

そして、このことからさらに、$x$次元座標の原点から距離$y$までの格子点を、距離$k (0≤k≤y)$ごとに分割すると、それらは$x-1$次元座標の原点から距離$k$までの格子点となっているということが分かります。

逆に言えば、一つの格子点を並べたものが直線の格子点、直線の格子点を距離$k$ごとに並べたものが平面の格子点、平面の格子点を距離$k$ごとに並べたものが立体の格子点、立体の格子点を距離$k$ごとに並べたものが４次元の格子点、、、と続く構造に任意の多次元座標の格子点はなっているということです。

直観的にはすぐには気付けない綺麗な構造ではないでしょうか？この構造からすると、組合せとは$1$から自然数を生み出す操作の一つの拡張と捉えられそうな気もしてくるのです。

自然数、順列、組合せ、パスカルの三角形、幾何、これらの間にはとても美しい法則が色々と眠っていて、より深い関係性を感じさせる事実がたくさんあります。興味があれば、ぜひ研究してみて下さい。

参考ページ：
Wikipedia：組合せ数学：概観と歴史
 Wikipedia：三角数
 パスカルの三角形の和公式、組合せと格子点

公開日：２０２０年１１月１３日
修正日：
２０２１年７月８日　「５－４．フェルマー・ワイルズの定理と格子点と道順」に【追記】を追加しました。

式と証明