1次、2次、高次の近似式についての解説
【目次】
0.はじめに
1.1次の近似式
2.2次の近似式
3.高次の近似式とテイラーの公式
はじめに
このページでは、高校数学の教科書(詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください。以下同じ。)の数学Ⅲ第4章「微分法の応用」第2節「速度と近似式」p.140発展「1次と2次の近似式」を深掘りしてみたいと思います。
1次の近似式
数学Ⅲ教科書p.139のように微分係数の定義から考え始めましょう。
\[f'(a)=\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}\]
微分係数は、\(x\)の増加分、つまり差分\(\Delta x= (a+h)-a = h\)あたりの\(y\)の増加分、つまり差分\(\Delta y = f(a+h)-f(a)\)との比
\[\frac{\Delta y}{\Delta x}\]
の極限でした。この比は、\(\Delta y\)を\(\Delta x\)で割っているので\(\Delta x\)を\(1\)としたときの\(\Delta y\)の増加分、つまり平均増加分(又は減少分、あわせて平均変化率)と捉えることができるので\(y\)の\(x\)による平均増加分の極限が微分係数と捉えることもできます。
そこで、\(f(a)+f'(a)h\)という式を考えると\(x=a\)あたりでの平均増加分(の極限)\(f'(a)\)に差分\(\Delta x\)(\(=h\))を掛けて、\(x\)の増加が1ではなく\(\Delta x\)であった場合の\(y\)の増加分を算出して、それを\(f(a)\)に足しているということになります。仮に、\(x=a\)以外でも常に\(f'(a)\)だけ\(x\)に対して同様に\(y\)が増加しているのであれば、\(x\)が\(\Delta x\)増加したときの\(y\)の増加分は\(\Delta y\)で表されるので\(\Delta y = f'(a)\Delta x\)が成立し、
\[f(a+\Delta x)=f(a)+\Delta y=f(a)+f'(a)\Delta x\]
つまり、
\[f(a+h)=f(a)+f'(a)h\]
が成立しているはずです。
関数\(f(x)\)が一次関数であればこの等式が成立しますが、一般的な関数\(f(x)\)では\(x=a\)以外では傾き\(f'(a)\)とは限らないので、誤差が生じます。これを誤差\(R\)とすると、
\[f(a+h)=f(a)+f'(a)h+R\ \ \ \ \cdots ①\]
が成立します。つまり、教科書では
\[f(a+h)\fallingdotseq f(a)+f'(a)h\]
と表されます。誤差\(R\)は、式①を変形して、
\[R=\{ f(a+h)-f(a) \}-f'(a)h\]
\(h\)で式全体を割ると、
\[\frac{R}{h}=\frac{f(a+h)-f(a)}{h}-f'(a)\]
と表され、誤差\(R\)は変数\(h\)によって変化する関数と考えることができるので両式の極限を取ると、
\[\lim_{h\to 0}R(h)=\lim_{h\to 0}\{ f(a+h)-f(a) \}-f'(a)h=0\]
\[\lim_{h\to 0}\frac{R(h)}{h}=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}-f'(a)=f'(a)-f'(a)=0\]
より\(h\)が\(0\)に近づくほど、つまり\(x=a\)に近づくほど誤差\(R(h)\)が\(0\)に近づいて行くことが分かります。誤差\(R(h)\)が\(h\)の大きさよりも速く小さくなっていくことも分かります。というのは、たとえば、誤差\(R(h)\)の関数が\(R(h)=1\)、\(R(h)=\sqrt h\)、\(R(h)= h\)、\(R(h)= h^2\)の場合を考えてみましょう。
\(R(h)=1\)の場合は、誤差が小さくならないので
\[\lim_{h\to 0}\frac{R(h)}{h}=\lim_{h\to 0}\frac{1}{h}=+\infty\]
と無限に発散してしまいます。
\(R(h)=\sqrt h\)の場合は、誤差\(R(h)\)は\(0\)に収束はしますが\(h\)の大きさよりも小さくなるのが遅いので(グラフを思い浮かべてください)
\[\lim_{h\to 0}\frac{\sqrt h}{h}=\lim_{h\to 0}\frac{1}{\sqrt h}=+\infty\]
と\(h\)での平均減少率はやはり発散してしまいます。
\(R(h)=h\)の場合は、誤差\(R(h)\)は\(0\)に収束はしますが
\[\lim_{h\to 0}\frac{h}{h}=\lim_{h\to 0}1=1\]
比率\(1\)で同じ速さで収束します。
\(R(h)=h^2\)の場合は、誤差\(R(h)\)も\(0\)に収束しますし、
\[\lim_{h\to 0}\frac{h^2}{h}=\lim_{h\to 0}h=0\]
と\(h\)での平均減少率も\(0\)に収束します。それだけ誤差\(R(h)=h^2\)の小さくなる速さが速いと考えられます。このように、誤差\(R(h)\)は\(0\)に収束するだけではなく、どれぐらいの速さで\(0\)に収束するかが論点になります。
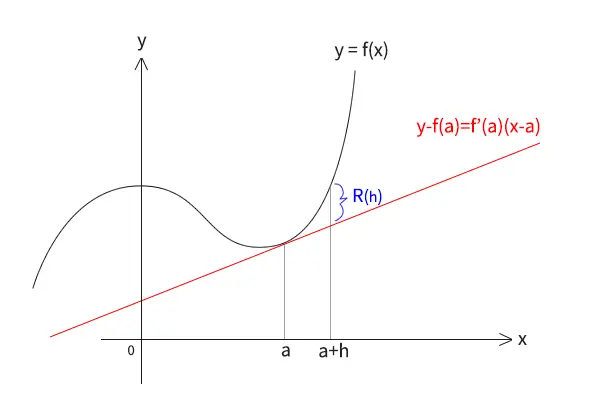
図1:1次の近似式
最後に変数\(x\)を変数\(h\)により\(x=a+h\)と表すと、式①は、
\[f(x)=f(a)+f'(a)(x-a)+R\]
と書けて、右辺の\(f(a)+f'(a)(x-a)\)部分は点\((a,f(a))\)で関数\(y=f(x)\)に接する一次関数のグラフ\(y=f(a)+f'(a)(x-a)\)です。つまり、一般の関数\(y=f(x)\)を一次関数\(y-f(a)=f'(a)(x-a)\)で近似していると考えられます。
2次の近似式
数学Ⅲ教科書p.140の発展では2次の近似式を紹介していて、一般の関数\(f(x)\)に対して2次関数\(g(x)=px^2+qx+r\)で条件\(f(a)=g(a),\ f'(a)=g'(a),\ f^{\prime\prime}(a)=g^{\prime\prime}(a)\)を満たす関数を\(x=a\)での2次の近似式として、その2次関数の近似式\(g(a+h)\)が、
\[g(a+h)=f(a)+f'(a)h+\frac{f^{\prime\prime}(a)}{2}h^2\ \ \ \cdots ②\]
と求められると主張しています。このように教科書ではよくある、説明の省略された記述があった場合には、難しいとは思いますが一度立ち止まって論点を整理してみることが大切です。その上で、自分で考えてみるか調査を試みてください。解決しなくとも気にせず試みてみることが大切です。この発展の場合には、次の3点ほどが主な論点になります。つまり、
ア.2次関数の上記条件より式②が本当に求められるのか、
イ.式②がどうして関数\(f(x)\)の近似式になっているのか(2次関数が上記条件を満たすとなぜ近似式になるのか)、
ウ.1次の近似式よりも2次の近似式の方が良い近似、つまり、近似式の値がより\(f(x)\)に近く誤差が少ないのか、
です。
教科書ではアの証明も省略されていますので、ここではまずアの証明をきちんと押さえておきましょう。あと、イとウについても厳密な話は次節に譲って直観的な理解について解釈をしてみましょう。
\[f(a)=g(a),\ f'(a)=g'(a),\ f^{\prime\prime}(a)=g^{\prime\prime}(a)\]
\[g(x) = px^2+qx+r,\ g'(x)= 2px+q,\ g^{\prime\prime}(x)=2p\]
なので
\[f^{\prime\prime}(a)=g^{\prime\prime}(a)=2p\]
より、
\[p=\frac{f^{\prime\prime}(a)}{2}\ \ \ \cdots③\]
であり、
\[f^{\prime}(a)=g^{\prime}(a)=2pa+q=2\cdot \frac{f^{\prime\prime}(a)}{2}\cdot a+q\]
より、
\[q=f'(a)-f^{\prime\prime}(a)a\ \ \ \cdots④\]
であり、
\[f(a)=g(a)=pa^2+qa+r=\frac{f^{\prime\prime}(a)}{2}\cdot a^2+\{f'(a)-f^{\prime\prime}(a)a\}a+r\]
より、
\[r=f(a)-\frac{f^{\prime\prime}(a)}{2}\cdot a^2 -\{f'(a)-f^{\prime\prime}(a)a\}a\ \ \ \cdots⑤\]
となります。上記の式③④⑤を\(g(x) = px^2+qx+r\)に代入して、
\[g(x)=\frac{f^{\prime\prime}(a)}{2}x^2+\{f'(a)-f^{\prime\prime}(a)a\}x+f(a)-\frac{f^{\prime\prime}(a)}{2}\cdot a^2 -\{f'(a)-f^{\prime\prime}(a)a\}a\]
\(x=a+h\)を代入して展開して整理すると、
\[g(a+h)=\frac{f^{\prime\prime}(a)}{2}(a+h)^2+\{f'(a)-f^{\prime\prime}(a)a\}(a+h)+f(a)-\frac{f^{\prime\prime}(a)}{2}\cdot a^2 -\{f'(a)-f^{\prime\prime}(a)a\}a \\
= \frac{f^{\prime\prime}(a)}{2}a^2+\frac{f^{\prime\prime}(a)}{2}\cdot 2ah+\frac{f^{\prime\prime}(a)}{2}h^2+f'(a)a-f^{\prime\prime}(a)a^2+f'(a)h-f^{\prime\prime}(a)ah+f(a)-\frac{f^{\prime\prime}(a)}{2}\cdot a^2 -f'(a)a+f^{\prime\prime}(a)a^2 \\
= \frac{f^{\prime\prime}(a)}{2}a^2-\frac{f^{\prime\prime}(a)}{2}\cdot a^2+\frac{f^{\prime\prime}(a)}{2}\cdot 2ah-f^{\prime\prime}(a)ah+\frac{f^{\prime\prime}(a)}{2}h^2+f'(a)a-f'(a)a-f^{\prime\prime}(a)a^2+f^{\prime\prime}(a)a^2+f'(a)h+f(a) \\
= \frac{f^{\prime\prime}(a)}{2}h^2+f'(a)h+f(a) \]
とたしかに式②が成立しました。
誤差\(R(h)\)を用いると、
\[f(a+h)=g(a+h)+R(h)=f(a)+f'(a)h+\frac{f^{\prime\prime}(a)}{2}h^2+R(h)\]
と表せて\(\lim_{h\to 0}R(h)=0\)が成立する近似式となっているというわけですが、次にイとウについての直観的な理解について解釈をしてみましょう。
まず、\(f(a)=g(a),\ f'(a)=g'(a)\)は1次の近似式で成立していた条件でした。2次の近似式はこれらに加えて\(\ f^{\prime\prime}(a)=g^{\prime\prime}(a)\)を条件とします。この条件は2階微分まで等しいというもので傾きの\(x=a\)における平均増加・減少分の極限を表します。つまり、傾きの増加・減少に関係する量です。傾きの増加が激しければ曲線は大きく曲がるし、増加が少なければ曲線の曲がりも少ないでしょう。つまり、2階の微分係数は曲線の曲がり方に関連する量になります。実は2階の微分係数単独では曲線の曲がり方を上手く表すことができませんが、1階の微分係数\(f'(a)=g'(a)\)まで合わせると曲がり方(曲率)を表すことができます。そのため2次の近似式の\(\ f^{\prime\prime}(a)=g^{\prime\prime}(a)\)という条件は、\(x=a\)における曲がり方にまで踏み込んだ等しさが成立していることを示しています。直観的には傾きに加えて曲がり方まで等しければ、近似がより正確になり\(x=a\)付近での誤差はより少ないはずだと感じられるのではないでしょうか。
数学Ⅲ教科書p.140では\(cos31^\circ\)の近似値を一次の近似式から\(0.8573\)と算出していますので、ここでは2次の近似式の計算を行ってみたいと思います。
\[cos31^\circ=cos(\frac{\pi}{6}+\frac{\pi}{180})=cos\frac{\pi}{6}-sin\frac{\pi}{6}\cdot \frac{\pi}{180} – \frac{cos\frac{\pi}{6}}{2}\cdot \{\frac{\pi}{180}\}^2=\frac{\sqrt 3}{2}-\frac{1}{2}\cdot \frac{\pi}{180}- \frac{\sqrt 3}{4}\cdot \{\frac{\pi}{180}\}^2\]
教科書の1次の近似値\(0.8573\)と数Ⅱ教科書の三角比表の\(cos31^\circ\)の値\(0.8572\)からは分かりませんが、Geogebra(ページを開いて紫色の近似ボタンを押してみてください)を使うと、\(cos31^\circ\)の値は\(0.8571673\)、1次の近似値は\(0.8572988\)、2次の近似値は\(0.8571669\)と2次の近似値の方がより良い近似となっています。
高次の近似式とテイラーの公式
1次の近似式①や2次の近似式②の右辺を観察すると、第一項は0次の近似式(定数関数\(y=f(a)\))で表れ、第二項は1次の近似式で表れ、第三項は2次の近似式で表れることが分かり、それぞれ第0階微分、第1階微分、第2階微分をすると最後の項の\(f(a),\ f'(a),\ f^{\prime\prime}(a)\)のみが残るように変数\(1,\ h,\ h^2\)の次数に合わせて係数の分母が\(1,\ 1,\ 2\)と続いているように見えます。(\(1=0!\)、\(1\cdot 1=1!\)、\(1\cdot 1\cdot 2=2!\))
そうすると、3次の近似式は条件\(f(a)=g(a),\ f'(a)=g'(a),\ f^{\prime\prime}(a)=g^{\prime\prime}(a)\)に続いて\(f^{\prime\prime\prime}(a)=g^{\prime\prime\prime}(a)\)を成立させるには、
\[\frac{f^{\prime\prime\prime}(a)}{1\cdot 1 \cdot 2 \cdot 3}h^3\]
を2次の近似式に追加すればその他の項は3階微分をすると消えてしまうので辻褄が合うことが分かります。
その先のn次の近似式についてもこの法則は成立するので、
\[\frac{f^{n}(a)}{n!}h^n\]
を新たな項として追加すれば\(f^{n}(a)=g^{n}(a)\)を成立させることができることが分かります。つまり、まだ理屈は分かりませんが、一般の関数\(f(x)\)の\(x=a\)に対して
\[g(a+h)=f(a)+f'(a)h+\frac{f^{\prime\prime}(a)}{2}h^2+\frac{f^{3}(a)}{3!}h^3+\ \cdots\ +\frac{f^{n}(a)}{n!}h^n\]
がn次の近似式となっているのではないかという予想が立てられます。一般の関数という定義が問題ですが、実際に高校数学で扱う多項式、三角関数、指数・対数関数などの初等関数においてはこの式はn次の近似式となっていて、それぞれ\(h^n\)よりも速く誤差が収束していきます。つまり、次数があがるほどより良い近似になっています。
この\(g(a+h)\)を以下のように\(x=a+h\)と置き直して正確な誤差項を付けた式をテイラーの公式と言います。
証明は高校数学の範囲を超えてしまいますが下記に、参考文献に挙げた高木貞治の『解析概論』p.66より引用しておきます。
【テイラーの公式】(表現上の改変をしました)
ある区間において\(f(x)\)は第n階まで微分可能とする。そうするとこの区間において、\(a\)は定点、\(x\)は任意の点とするとき
\[f(x)=f(a)+(x-a)\frac{f'(a)}{1!}+(x-a)^2\frac{f^{\prime\prime}(a)}{2!}+(x-a)^3\frac{f^{3}(a)}{3!}+\ \cdots\ +(x-a)^{n-1}\frac{f^{n-1}(a)}{(n-1)!}+(x-a)^{n}\frac{f^{n}(\xi)}{n!}.\]
ただし
\[\xi=a+\theta (x-a),\ \ \ \ 0<\theta<1.\]
つまり、\(\xi\)は\(a\)と\(x\)の中間のある値である。
が成立します。テイラーの公式の面白い点は、剰余項(誤差項)\(R(x,n)=(x-a)^{n}\frac{f^{n}(\xi)}{n!}\)の評価で\(x\rightarrow a\)の時に誤差が\(0\)に収束するだけではなく(\(\lim_{x\to a}R(x)=0\))、\(x\)を固定すれば\(\theta\)の取りえる範囲でたとえば\(f^{n}(\xi)\)の上限が定まってしまうような関数の範囲では、\(n\rightarrow \infty\)と次数を増やしても、階上は冪乗よりも急速に増加するので剰余項\((x-a)^{n}\frac{f^{n}(\xi)}{n!}\)が\(0\)に収束してしまいます(\(\lim_{n\to \infty}R(n)=0\))。つまり、次数が無限に続く多項式、冪級数と言いますが、冪級数で関数を表すことができます。それもある区間において「\(f(x)\)は第\(1,2,3, \cdots\)階まで微分可能」で「剰余項\(R(n)\)が\(0\)に収束する」必要があるとはいえ、各関数に対応する冪級数を特徴づけるのは各項の係数の中のi階(\(i=1,2,3, \cdots\))の微分係数\(f^{i}(a)\)の部分だけであり、それは点\(x=a\)(付近)の各関数の性質(第\(1,2,3, \cdots\)階の微分係数)だけで決まってしまうということです。
つまり、ある区間において「\(f(x)\)は第\(1,2,3, \cdots\)階まで微分可能」で「剰余項\(R(n)\)が\(0\)に収束する」のであれば、その区間全体のグラフの形がとても狭い範囲の点\(x=a\)(付近)の各関数の性質(第\(1,2,3, \cdots\)階の微分係数)だけで決まってしまうという不思議な自然法則が関数の極限にはあるということを示しています。この不思議な性質に魅せられて解析学はこの先にさらに面白い発展を続けて行きます。
以上のように教科書の発展や研究、コラム等はその先に重要で面白い内容がありますよという示唆だと考えて深掘りしてみることをお勧めします。多くの場合は数学の実用にはもちろんですが、大学受験等にも役立ったり必要となったりする内容になります。証明や誤差の評価などに興味のある方は『解析概論』を読んでみても良いですし、『解析概論』が難しい場合にはこだわる必要はなく、様々な難易度に合わせた書籍が図書館や本屋にたくさんありますので手に取ってみましょう(Web上にもたくさん解説が掲載されています)。
本サイトでテイラーの公式の証明について解説するかは、高校数学の範囲を越えてしまいますので一考を要します。
参考文献:
『定本 解析概論』高木貞治 岩波書店
著者:L&M個別オンライン教室 瀬端隼也
公開日:2025年1月11日
修正日:-



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。