三角形の辺の長さと角の大きさの関係
このページでは、三角形において、二つの角の角度の大小関係はその向かい合う辺の長さの大小関係と一致することを、きちんと根拠を示しながら証明します。
特に、角度がより大きければ、その向かい合う辺もより長いことについては、「背理法での証明」と「ピタゴラスの定理を用いた証明」の二つの証明を紹介します。
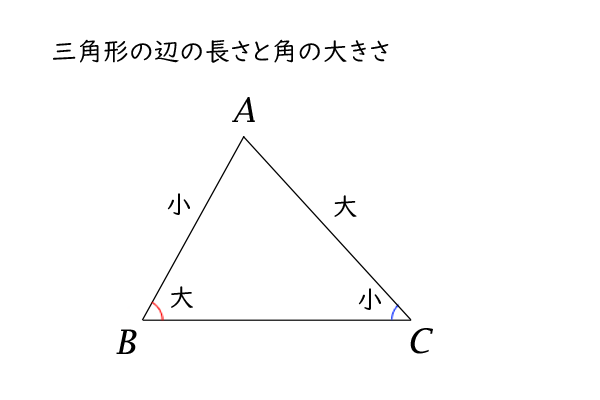
図1:三角形の辺の長さと角の大きさの関係、長さ→角度、角度→長さ
まず、三角形の辺の長さと角の大きさの関係をきちんと表現すると、次の【命題:三角形の辺の長さと角の大きさの関係】が成り立ちます。
【命題:三角形の辺の長さと角の大きさの関係】
三角形\(ABC\)において、
\[\angle B \geq \angle C \Leftrightarrow AC \geq AB \tag{1}\]
が成り立つ。特に、等号について、
\[\angle B = \angle C \Leftrightarrow AC = AB \tag{2}\]
が成り立つ。
【証明】
まず、式(1)の右辺から左辺の向き(長さ→角度)を証明しましょう。
特に、その等号の式(2)の右辺から左辺の向き(長さ→角度)の証明から行います。
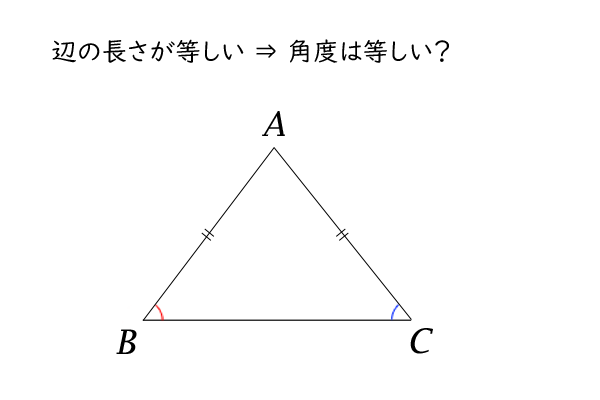
図2:二等辺三角形(長さ→角度)
\(\angle A\)の二等分線\(l\)を引くと、辺\(BC\)との交点があるはずなので、それを点\(D\)とします。
そうすると、\(AC = AB\)であった場合、三角形\(ADB\)と三角形\(ADC\)は、辺\(AD\)を共有し、\(\angle BAD = \angle CAD \)より、二辺挟角が等しいので、合同になります。
したがって、\(\angle ABD = \angle ACD \)が成り立ちました。
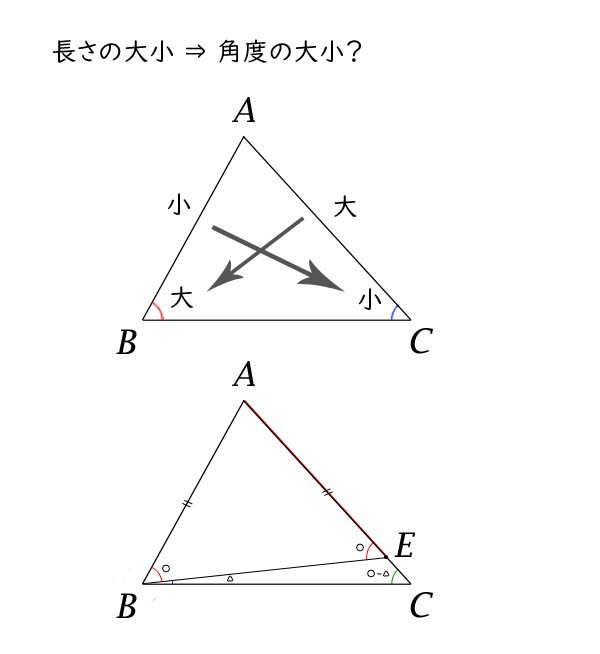
図3:長さ→角度
次に、\(AC \gt AB\)であった場合に、点\(A\)を端点として辺\(AC\)上に線分\(AE\)の長さが\(AE=AB\)となるように点\(E\)を取ることができます。
三角形\(ABE\)について、今、証明した式(2)の右辺から左辺の向きを当てはめると、
\[\angle ABE = \angle AEB \tag{3} \]
が成り立ちます。
ここで、\(\angle AEB\)と\(\angle BEC\)は一直線上にあるので、
\[\angle BEC = 180^\circ – \angle AEB \tag{4}\]
が成り立ち、
三角形\(EBC\)において、三角形の内角の和は\(180^\circ\)なので、
\[\angle ACB = 180^\circ – \angle EBC – \angle BEC \tag{5}\]
が成り立ちます。
式(4)(5)より、
\[\angle ACB = 180^\circ – \angle EBC – (180^\circ – \angle AEB) = \angle AEB – \angle EBC \tag{6}\]
が成り立ちます。
一方で、\(\angle ABC\)において、
\[\angle ABC = \angle ABE + \angle EBC \tag{7}\]
が成り立ちます。
式(3)(6)(7)より、
\[\angle ABC = \angle ABE + \angle EBC \gt \angle AEB – \angle EBC = \angle ACB\]
が成り立ち、式(1)の右辺から左辺の向き(長さ→角度)の証明ができました。
それでは、次に、式(1)の左辺から右辺の向き(角度→長さ)を証明したいと思います。
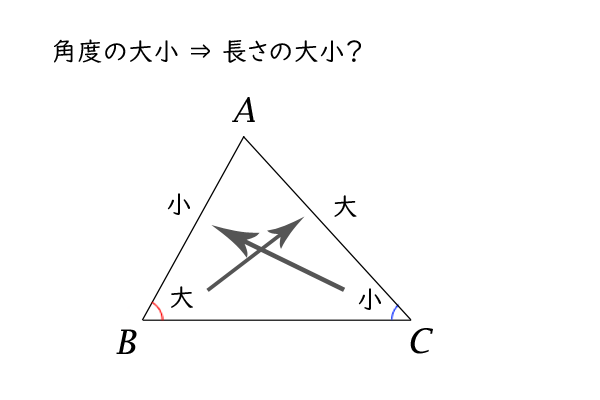
図4:角度→長さ
まずは、等号が成り立たない場合から証明したいとします。
つまり、\(\angle B \gt \angle C\)の場合です。
仮に、この場合に\(AC \leq AB\)とすると、すでに証明した式(1)の右辺から左辺の向きを適用すると、
\[\angle B \leq \angle C\]
が成り立ちますが、これは\(\angle B \gt \angle C\)と矛盾します。
したがって、
\[AC \gt AB\]
が成り立つことが分かり証明できました。
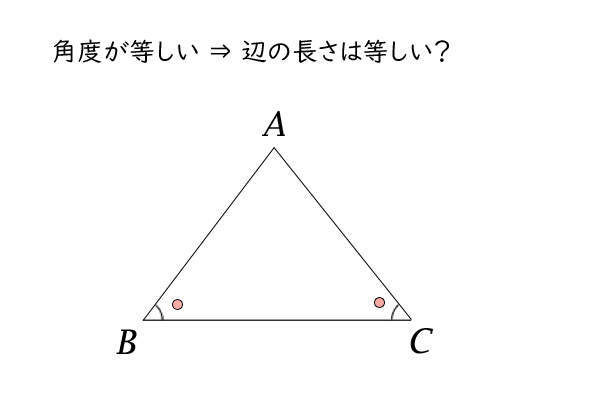
図5:二等辺三角形(角度→長さ)
次に、等号が成り立つ場合を証明したいとします。
つまり、\(\angle B = \angle C\)の場合です。
仮に、この場合に、\(AC \lt AB\)又は\(AC \gt AB\)とすると、すでに証明した式(1)の右辺から左辺の向きより、
\(\angle B \lt \angle C\)又は\(\angle B \gt \angle C\)となるので、\(\angle B = \angle C\)と矛盾します。
したがって、\(AC \geq AB\)かつ\(AC \leq AB\)であり、つまり、\(AC = AB\)であることが証明できました。□
式(1)の左辺から右辺の向きの証明には、ピタゴラスの定理を用いたものをあります。次に、その証明も行いましょう。
【証明2】
【命題:三角形の辺の長さと角の大きさの関係】の式(1)の左辺から右辺の向き(角度→長さ)の別証明です。
つまり、\(\angle B \geq \angle C\)の場合を考えます。
点\(A\)から辺\(BC\)に垂線が引ける(参照:円と直線の距離と位置関係、特に交点、接点、接線について:4-2.垂線の定義、存在、一意性、距離)ので、その足を点\(F\)とします。
三角形\(ABF\)と三角形\(ACF\)は、直角三角形なので、それぞれ、
\[\angle BAF = 90^\circ – \angle B\]
\[\angle CAF = 90^\circ – \angle C\]
が成り立ちます。
ここで、\(\angle B \geq \angle C\)なので、
\[\angle BAF \leq \angle CAF \tag{1}\]
が成り立ちます。
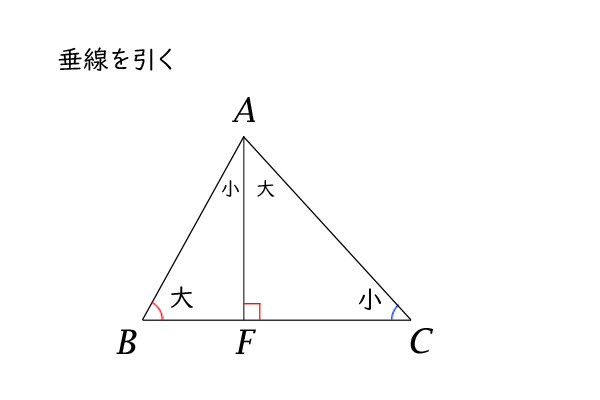
図6:三角形に垂線を引く
今、点\(A\)と垂線\(AF\)と直線\(BC\)に着目しましょう。
点\(A\)から直線\(BC\)へ、点\(F\)とは異なる点\(H\)を取って、線分\(AH\)を引きます。
次に、点\(A\)から線分\(AH\)と同じ側に\(\angle FAH\)よりも大きく\(90^\circ\)よりも小さい角度を垂線\(AF\)と持つ直線\(m\)を引きます。
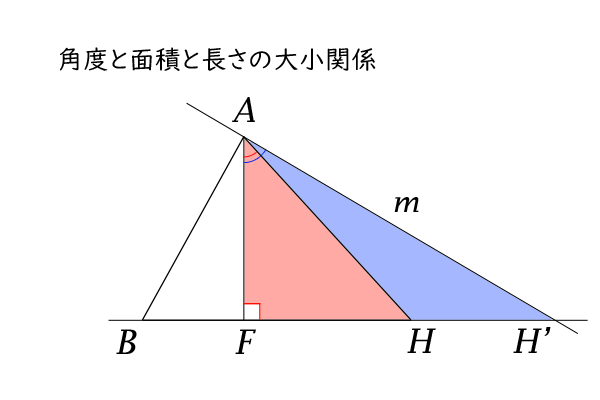
図7:角度と面積と長さの大小関係
直線\(m\)は、\(90^\circ\)よりも小さい角度なので、直線\(BC\)と平行ではなく交点を持ちます。その交点を点\(H^{‘}\)とします。
二直線は2つの交点を持たないので、点\(A\)を端点とする半直線\(AH^{‘}\)は半直線\(AH\)と点A以外で交点を持ちません。
したがって、三角形\(AH^{‘}F\)は三角形\(AHF\)を包含します。
ここで、三角形\(AH^{‘}F\)と三角形\(AHF\)について、底辺\(AF\)を共有する直角三角形とみなせるので、三角形の面積の大小関係より、\(FH^{‘} \gt FH\)が分かりました。
以上のことから、点\(A\)から出る直線は、垂線\(AF\)とのなす角が大きいほど、直線\(BC\)上において点\(F\)から遠い交点を持つことが分かりました。
これと式(1)より、
\[BF \leq CF \tag{2}\]
が成り立ちます。
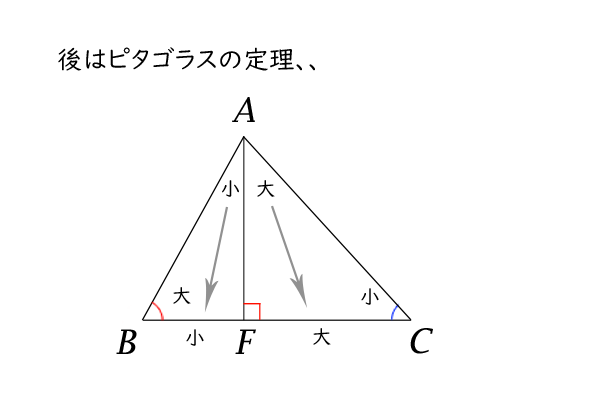
図8:後はピタゴラスの定理、、
三角形\(ABF\)と三角形\(ACF\)は、直角三角形なので、ピタゴラスの定理を適用すると、
\[AB^{2} = AF^{2} + BF^{2} \tag{3}\]
\[AC^{2} = AF^{2} + CF^{2} \tag{4}\]
式(2)(3)(4)より、
\[AB \leq AC\]
が成り立つことが証明できました。□
著者:L&M個別オンライン教室 瀬端隼也
公開日:2019年10月9日
修正日:ー



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。