空間における平行な直線の推移関係について

【目次】
１．空間における平行な直線の推移関係
  １－１．なぜ重要なのか
  １－２．勉強の仕方、命題の背景
２．平行線の定義の確認
  ２－１．二直線のねじれの位置とは
    ２－１－１．前提命題：直線の決定と平面の決定
  ２－２．空間と平面における二直線の位置関係
３．空間における平行な直線の推移関係の証明
  ３－１．二直線が同一平面上にあること
  ３－２．二直線が交点を持たないこと
４．発展：一意性、平面推移律、空間推移律－平行３命題の同値性
  ４－１．平行線に関する各命題の解説
  ４－２．３命題の同値性の証明

空間における平行な直線の推移関係

空間における平行な直線には、高校数学の空間図形の範囲において次の重要な命題が成り立ちます。

【命題：空間における平行な直線の推移関係】
空間において二直線\(m,n\)が同じ一直線\(l\)に平行で、その三直線が同一平面上になければ二直線\(m,n\)も互いに平行である。

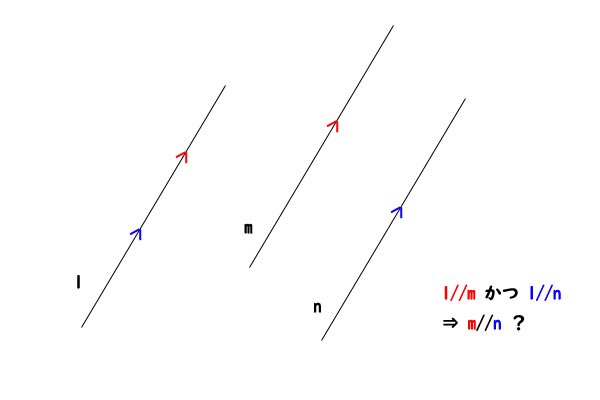
図１：空間における平行な直線の推移関係

ちなみに、推移関係（推移律）とは、\(A\)と\(B\)にある関係\(x\)が成り立ち、\(B\)と\(C\)にもある関係\(x\)が成り立つならば、\(A\)と\(C\)にもある関係\(x\)が成り立つ、このような関係自体を表すと共に、このような場合に関係\(x\)は推移関係（推移律）を満たすと言います。上記の命題であれば、\(A\)を\(m\)、\(B\)を\(l\)、\(C\)を\(n\)、関係\(x\)を「平行」に置き換えて考えてください。

なぜ重要なのか

最も重要な応用は、数学Ａの教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）では、証明なしで言及されていますが、「二直線のなす角」を空間図形でも定義することができることです。

もちろん、空間図形でも二直線が同一平面にある場合には、二直線が一致する場合や平行である場合を角度\(0^\circ\)と定義するかどうかという問題もありますが、その他の場合、つまり、二直線が一つの交点を持つ場合には、通常の定義での二直線の角度を定義することができます。

一方、空間図形で「二直線のなす角」の定義が問題になるのは、二直線が同一平面にない場合です。つまり、二直線がねじれの位置にある場合にどのように角度を定義すれば良いのか、というよりも定義できるのかという疑問が生じるわけです。

【命題：空間における平行な直線の推移関係】を証明すれば、この空間図形で二直線がねじれの位置にある場合の角度を定義することができます。空間図形における「二直線のなす角」の定義は、別ページ：空間図形における二直線のなす角と二平面のなす角を参照ください。

ちなみに、この【命題：空間における平行な直線の推移関係】を使わずとも「二直線のなす角」を空間図形で定義する方法は他にもあると思います。しかし、少なくともこのサイトでは、そのための準備としてこのページを作成していますし、筋道として妙手とは言えないかもしれませんが、納得はできるものにしてあります。

それ以外にも重要な応用があるということは、原理的にも重要な命題であって、その重要性の端緒には後述の発展：一意性、平面推移律、空間推移律－平行３命題の同値性で触れています。

勉強の仕方、命題の背景

証明の手順や方法は、色々とあります。以前にも書きましたが、興味のある方は、高校の図書館、近くの本屋や公共図書館に適当な教科書がなくても、都道府県の図書館、国会図書館には必ず適当な教科書がたくさんあります。何か調べ物をするために図書館に通う習慣を身に付けることは、勉強を深めていくためにはとても大切な習慣であると思います。ぜひ、この機会にお気に入りの図書館を見つけてみてください。

その際、高校数学の幾何でまず確認してみて損のないのは、やはりユークリッドの原論です。この【命題：空間における平行な直線の推移関係】も、１１章命題９で明確に証明されています。ただ、ユークリッドの原論では、【命題：空間における平行な直線の推移関係】における二直線\(m,n\)が同一平面にあることを証明するために、かなり多くの命題を要しているので、この一ページで紹介するのは難しいと思いました。

ぜひ、ご自分の手に取り確認してみてください。残念ながらウェブ上で日本語の完訳のユークリッドの原論を見つけることはできませんでした。英語では幾つかあるようです。残念ながら日本語は、学問や科学技術の世界ではマイナーな言語です。本格的に学問をしたい方や技術を学びたい方は、早めにまず英語をマスターし、その後、余裕があればフランス語やドイツ語、自分の学ぶ学問領域に関係する言語や学問上重要となる古典的な言語、例えばラテン語やギリシャ語などに興味を向けてみることをお勧めします。

このページでの証明は、ユークリッドの原論よりもかなり短い代わりに少し抽象的で分かりにくいかもしれません。ただ、手順を一つ一つ追っていけば、論理的な飛躍のないように注意して書いていますので、推論が追えなくなるということは少ないのではないかと期待しています。大学での勉強に入ればさらに抽象化することで、逆に、シンプルになり見通し良く分かりやすい証明を書くことができると思います。ただ、高校数学の範囲を大幅に超えてしまいますし、その準備を理解することが大変になるだろうと思います。

平行線の定義の確認

空間図形における平行線と言っても、結局は平行という概念は平面図形における平行線の定義しかありません。このことを理解するポイントは、空間における二直線のねじれの位置をきちんと理解することにあると思います。

二直線のねじれの位置とは

まず、出発点として空間における二直線がいずれかの同一平面上にあった場合、それは平面図形における位置関係を適用できるので、二直線は一致するか、一つの交点を持つか、平行となるかのいずれかだと分かります。

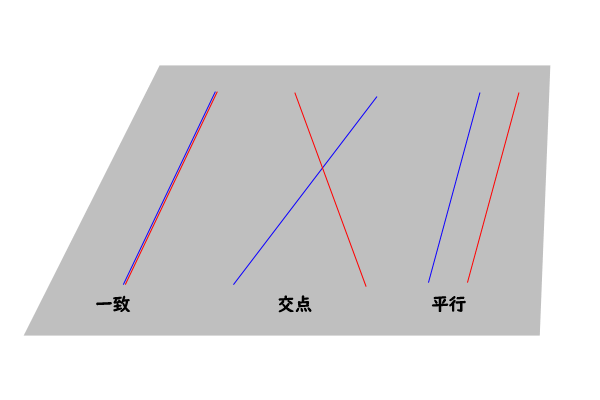
図２：同一平面上の二直線

つまり、空間において二直線がいずれかの同一平面上にあった場合には、二直線がねじれの位置になることはないのです。

したがって、二直線がねじれの位置あるためには、少なくともすべての平面がその二直線を含んでいないという条件が必要になります。

それでは、すべての平面がその二直線を含んでいない場合で、ねじれの位置でもない場合とは何でしょうか。

ねじれの位置でもない場合とは、二直線に交点がある場合か、二直線が平行である場合のどちらかですが、まずは、二直線に交点がある場合を考えてみましょう。

前提命題：直線の決定と平面の決定

ここで、次の二つの命題を前提としますと、

【命題：直線の決定】
同一点上にない２点を含む直線はただ一つ存在する。

図３：直線の決定

と、

【命題：平面の決定】
同一直線上にない３点を含む平面はただ一つ存在する。

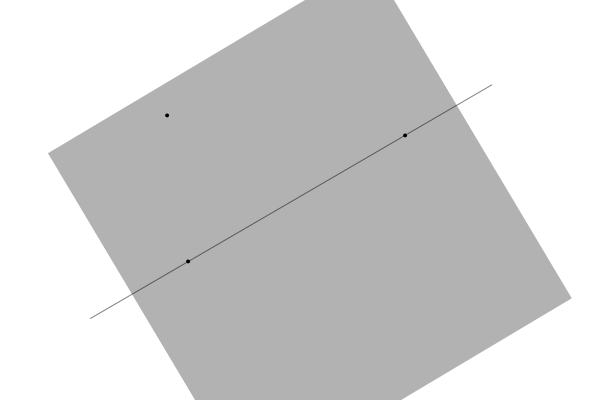
図４：平面の決定

少なくとも異なる二直線\(l,m\)が交点\(A\)を持っていれば、その二直線上に同一直線上にない３点\(A\),\(l\)上の\(B\),\(m\)上の\(C\)を取ることができるので、その３点を含む平面\(\alpha\)がただ一つ存在します。そのため、平面\(\alpha\)内において点\(A,B\)と点\(A,C\)を含む直線\(AB\)と直線\(AC\)がただ一つ引けますし、それ以外に点\(A,B\)と点\(A,C\)を含む直線は引けません。したがって、直線\(AB\)は直線\(l\)と一致し、直線\(AC\)は直線\(m\)と一致し、くわえて二直線\(l,m\)は平面\(\alpha\)に含まれます。（注意：この証明には、色々と暗黙の前提がありますが、深堀に過ぎるのでこれ以上は明示しません。）

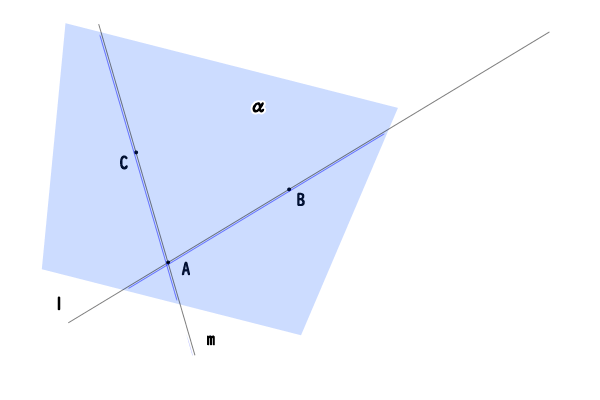
図５：二直線に交点がある場合

したがって、異なる二直線が交点を持っていれば、二直線は同一平面に含まれることになります。

そうすると、二直線が交点を持っている場合は除外されるので、後は、平行である場合しかありません。

しかし、仮にあるとするならば、すべての平面がその二直線を含んでいない場合で、平行である場合とは何でしょうか？

少なくとも、すべての平面がその二直線を含んでいないので、平面図形で適用された平行に関する法則はまったく無関係ということになります。

つまり、すべての平面がその二直線を含んでいない場合で、平行である場合を想定したとしても、それと平面図形で適用された平行とは、共通項が二直線が交点をもっていないこと、それのみなのです。

一方で、平面図形で適用された平行と、空間図形における二直線がねじれの位置にあることの共通項も交点をもっていないことのみです。

そうであるならば、すべての平面がその二直線を含んでいない場合で、平行である場合の存在を想定しても何の意味もないわけです。あるいは、そのような平行の定義は何も差別化できないとも言えます。

したがって、すべての平面がその二直線を含んでいない場合には、ねじれの位置しかないということになります。つまり、すべての平面がその二直線を含んでいないことが、二直線がねじれの位置にあることの必要十分な条件になります。

空間と平面における二直線の位置関係

そうすると、空間にある二直線の位置関係は、次の４つに整理されます。

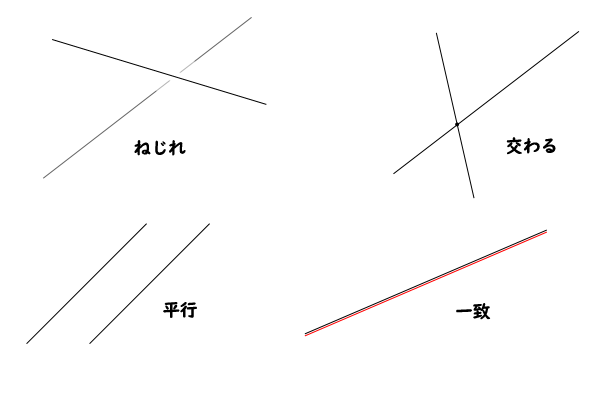
図６：空間にある二直線の位置関係

【定義：ねじれの位置にある二直線】
同一平面に含まれない二直線（交わらない、仮に交わると上述の証明より同一平面に含まれるので矛盾します。）

【定義：交わる直線】
同一平面に含まれる互いに交わる二直線

【定義：平行線】
同一平面に含まれる互いに交わらない二直線

【定義：一致する二直線】
二直線が一直線に一致する

ちなみに、平面にある二直線の位置関係は、次の３つに整理されます。

図２再掲：平面にある二直線の位置関係

【定義：平面内の交わる直線】
互いに交わる二直線

【定義：平面内の平行線】
互いに交わらない二直線

【定義：平面内の一致する二直線】
二直線が一直線に一致する

したがって、例えば、空間図形で平行線は同一平面に含まれるか？という疑問を持ったとすると、同一平面に含まれない２直線に平行という言葉を名付けても意味がないという答えになります。

空間における平行な直線の推移関係の証明

それでは、【命題：空間における平行な直線の推移関係】を証明したいと思います。

【命題：空間における平行な直線の推移関係】
空間において二直線\(m,n\)が同じ一直線\(l\)に平行で、その三直線が同一平面上になければ二直線\(m,n\)も互いに平行である。

【証明】

二直線が同一平面上にあること

同一平面上にない二直線はねじれの位置にあり、二直線が平行線であるためには同一平面上にあることが必要条件であることを見てきました。

そこでまず、二直線\(m,n\)が同一平面上にあることを示します。

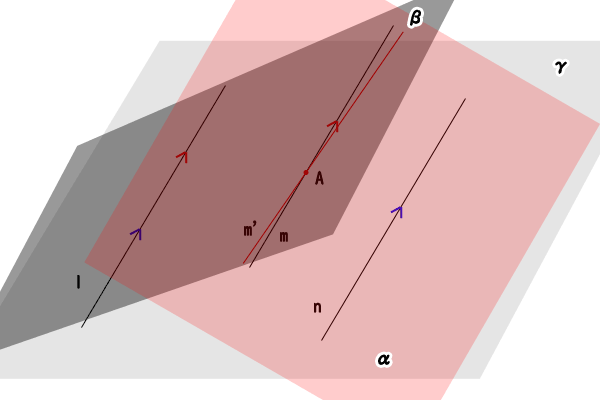
図７：空間における平行な直線の推移関係：同一平面の証明

直線\(m\)上のある点を\(A\)とします。

直線\(n\)と点\(A\)を含む平面は、【命題：直線の決定】と【命題：平面の決定】よりただ一つ存在するので、これを平面\(\alpha\)とします。（証明は、交わる二直線が同一平面に含まれることを示した先述の証明とほぼ同じです。）

二直線\(l,m\)は平行なので同一平面に含まれており、これを平面\(\beta\)とします。

二直線\(l,n\)も平行なので同一平面に含まれており、これを平面\(\gamma\)とします。

ここで前提として、空間において二平面の位置関係は、「二平面が一致するか」、「二平面が一直線を共有するか」、「二平面が交わらないか」のいずれかであるとすると、

平面\(\alpha\)と平面\(\beta\)は共有点\(A\)を持つので、平面\(\alpha\)と平面\(\beta\)は一直線を共有することになります。この直線を直線\(m^{‘}\)とします。

ここから仮に、二直線\(m,n\)が同一平面上にないと仮定して推論を進め、矛盾を導き出すことで証明を行いたいと思います。

二直線\(m,n\)が同一平面上になければ、直線\(n\)を含む平面\(\alpha\)は、直線\(m\)を含みません。したがって、平面\(\alpha\)に含まれる直線\(m^{‘}\)は、直線\(m\)とは異なる直線となります。つまり、\(m \neq m^{‘}\)が成り立ちます。

一方、平面\(\beta\)は直線\(l,m,m^{‘}\)を含み、直線\(m,m^{‘}\)は点\(A\)で交わります。

ここで前提として、ある点\(X\)と点\(X\)を通らない直線\(a\)の組について、点\(X\)を通り直線\(a\)に平行な直線はただ一つであるとすると（参照：ページ後方記載の発展：一意性、平面推移律、空間推移律－平行３命題の同値性）、

平面\(\beta\)において、直線\(l\)と直線\(m\)は平行で、直線\(m,m^{‘}\)は点\(A\)で交わり、\(m \neq m^{‘}\)なので、直線\(l\)と直線\(m^{‘}\)は平行になりません。さもなければ、一点を通る平行線が二つあることになり前提に矛盾します。

したがって、直線\(l\)と直線\(m^{‘}\)は交点を持ち、その交点を点\(B\)とします。

点\(B\)は直線\(m^{‘}\)に含まれ、直線\(m^{‘}\)は平面\(\alpha\)に含まれるので、直線\(l\)と平面\(\alpha\)は点\(B\)を共有します。

ここで、仮に直線\(l\)が平面\(\alpha\)に含まれるとすると、

もともと平面\(\beta\)は、直線\(l\)と直線\(m\)を含み、したがって点\(A\)を含みますし、
平面\(\alpha\)も、点\(A\)と直線\(l\)を含むことになるので、【命題：平面の決定】より、平面\(\alpha\)と平面\(\beta\)が一致します。
そうすると、直線\(l\)と直線\(m\)と直線\(n\)が同一平面内にあることになり、命題の条件と矛盾します。

したがって、直線\(l\)は平面\(\alpha\)に含まれないことが分かりました。

ここで前提として、空間において直線と平面の位置関係は、「平面が直線を含むか」、「平面と直線が一点を共有するか」、「平面と直線が交わらないか」のいずれかであるとすると、

直線\(l\)は平面\(\alpha\)と点\(B\)のみによって交わることが分かりました。

さらにここで、仮に平面\(\alpha\)において直線\(n\)が点\(B\)を通るとすると、

直線\(l\)と直線\(n\)は点\(B\)を持つことになり、直線\(l\)と直線\(n\)が平行であるという命題の条件と矛盾します。

したがって、直線\(n\)は点\(B\)を通らないことが分かります。

そして、ここが大詰めですが、
平面\(\gamma\)は、直線\(n\)を含み、直線\(l\)を含んでいるので点\(B\)を含んでいますし、
平面\(\alpha\)も、直線\(n\)を含み、点\(B\)を含んでいます。
くわえて、直線\(n\)は点\(B\)を通らないので、【命題：平面の決定】より、平面\(\gamma\)と平面\(\alpha\)が一致します。

しかしながら、そうすると、直線\(l\)が平面\(\alpha\)に含まれることになり、直線\(l\)が平面\(\alpha\)と点\(B\)のみによって交わることに矛盾してしまいます。

したがって、二直線\(m,n\)が同一平面上にあることが分かりました。

二直線が交点を持たないこと

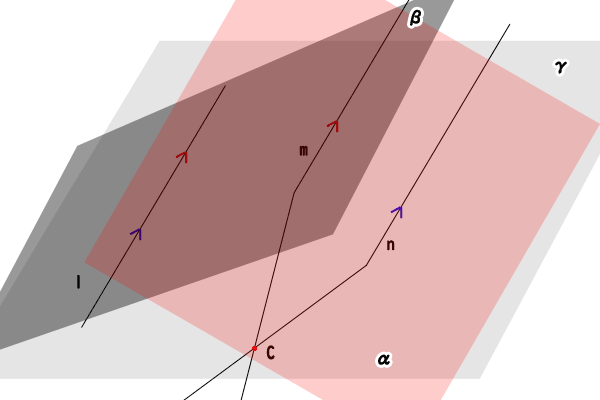
図８：空間における平行な直線の推移関係：交点のないことの証明

次に、二直線\(m,n\)が交点を持たないことを示します。

仮に、二直線\(m,n\)が交点\(C\)を持つとすると、

平面\(\beta\)は、直線\(l\)を含み、直線\(m\)を含んでいるので点\(C\)を含んでいます。
平面\(\gamma\)も、直線\(l\)を含み、直線\(n\)を含んでいるので点\(C\)を含んでいます。
直線\(l\)と直線\(m\)は平行であり、あるいは直線\(l\)と直線\(n\)は平行なので、点\(C\)は直線\(l\)上にない点であり、
したがって、【命題：平面の決定】より平面\(\beta\)と平面\(\gamma\)は一致します。

そうすると、直線\(l,m,n\)が同一平面上にあることになり、命題の条件と矛盾します。

したがって、二直線\(m,n\)が同一平面上にあり、平行であることが分かりました。□

発展：一意性、平面推移律、空間推移律－平行３命題の同値性

平行線に関する各命題の解説

まず、平面における平行線についての重要な命題は、次の二つに分けられます。

①【命題：平行線の存在】
平面上のすべての点\(A\)について、その点\(A\)を通らない直線\(l\)と交わらず、かつ、点\(A\)を通る直線\(m\)が引ける。

②【命題：平行線の一意性】
上記の直線\(m\)は、点\(A\)と直線\(l\)の各組についてただ一つのみ引ける。

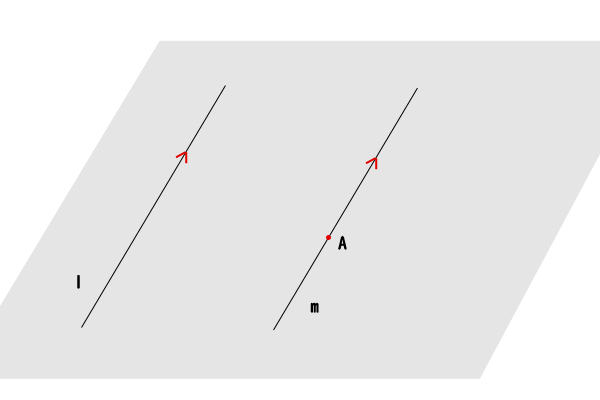
図９：平行線の命題①②

命題①は、平行線があること、命題②は、それが一つだけであること、を主張しています。

さらに、次の平面における平行線についての命題が考えられます。

③【命題：平面における平行な直線の推移関係】
平面において二直線\(m,n\)が同じ一直線\(l\)に平行ならば、二直線\(m,n\)も互いに平行である。
（空間において二直線\(m,n\)が同じ一直線\(l\)に平行で、その三直線が同一平面上にあれば二直線\(m,n\)も互いに平行である。）

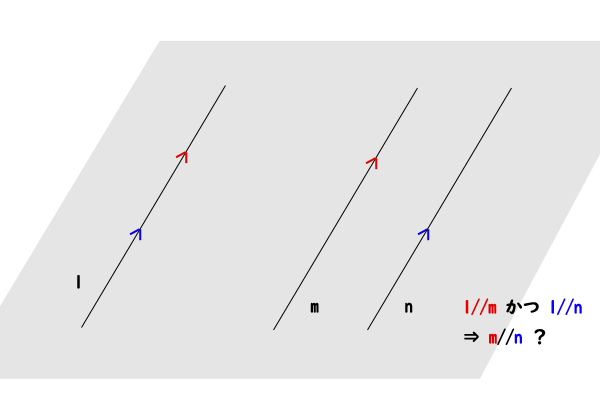
図１０：平行線の命題③

ここで、発展として示すことは、この命題③と命題②が同値になることです。

さらに、このページで証明した空間における平行線についての命題が命題②と命題③と同値になることを示したいと思います。

つまり、

④【命題：空間における平行な直線の推移関係】
空間において二直線\(m,n\)が同じ一直線\(l\)に平行で、その三直線が同一平面上になければ二直線\(m,n\)も互いに平行である。

図１再掲：平行線の命題④

とすると、命題②と命題③と命題④が同値というわけです。

特に、命題④は空間における命題なのに、平面における命題と同値、つまり幾何学の前提として置き換えられるという点が興味深いというお話です。

ちなみに、人の世界に対する幾何学的な理解というのは、まったく発展途上であり、点、直線、平面、空間に分けるという捉え方自体、数千年前に見いだされたとても古い枠組みと言えます。

物理的に極大、極小の世界を見渡せば、点、直線、平面、空間という枠組みにおいて成立すると一般的に仮定された命題が、どうも当てはまらない、ということはすでにたくさん検証されています。

平行線にまつわる命題は、近世から検証が行われてきましたし、先述の【命題：直線の決定】や点、直線、平面、空間に分けるという枠組み自体さえ、検証の対象になりうるのが数学の面白いところです。

それでは、証明を行いたいと思います。

３命題の同値性の証明

まず、前節の空間における平行な直線の推移関係の証明において、命題④の証明の根拠として命題②を使用していますので（この箇所です）、命題②\( \Rightarrow \)命題④はすでに示しました。

次に、命題④\( \Rightarrow \)命題③を示します。

【証明】

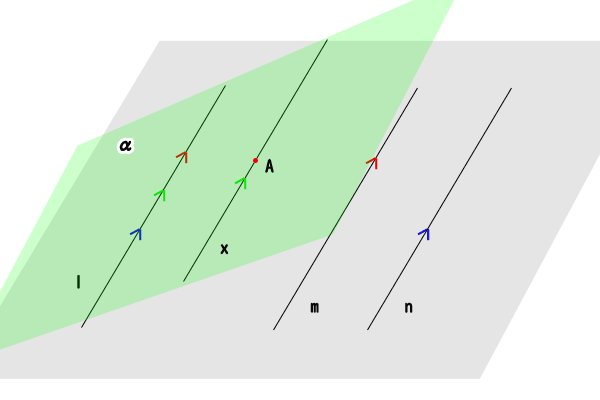
図１１：平行線の命題④\( \Rightarrow \)命題③

まず、直線\(l.m,n\)が同一平面上にありますが、直線\(l\)を含み、直線\(m,n\)を含まない平面\(\alpha\)を取ります。

平面\(\alpha\)において、直線\(l\)に含まれない点\(A\)を取ります。そうすると、命題①より点\(A\)を通り、直線\(l\)に平行な直線\(x\)を引くことができます。

直線\(l\)と直線\(m\)は平行であり、直線\(l\)と直線\(x\)は平行であり、三直線\(l,m,x\)は同一平面に含まれないので、命題④より直線\(m\)と直線\(x\)が平行であることが分かります。

同様に、直線\(l\)と直線\(n\)は平行であり、直線\(l\)と直線\(x\)は平行であり、三直線\(l,n,x\)は同一平面に含まれないので、命題④より直線\(n\)と直線\(x\)が平行であることが分かります。

そうすると、
直線\(x\)と直線\(m\)は平行であり、直線\(x\)と直線\(n\)は平行であり、三直線\(x,m,n\)は同一平面に含まれないので、命題④より直線\(m\)と直線\(n\)が平行であることが分かりました。□

最後に、命題③\( \Rightarrow \)命題②を示します。

【証明】

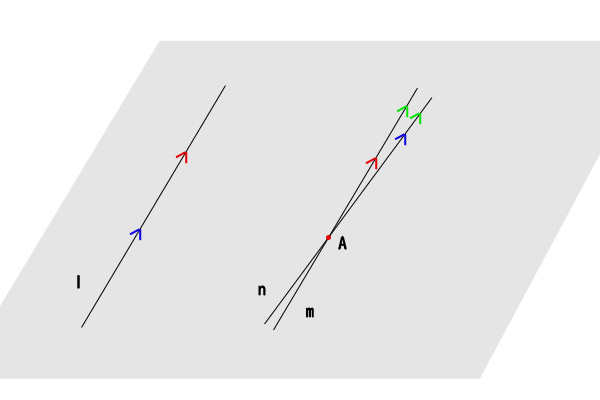
図１２：命題③\( \Rightarrow \)命題②

仮に、直線\(m\)以外に、点\(A\)を通り直線\(l\)と交わらない直線\(n\)も引けたとします。

そうすると、命題③より、平面において二直線\(m,n\)が同じ一直線\(l\)に平行なので、二直線\(m,n\)も互いに平行になります。つまり、二直線\(m,n\)は交点を持ちません。

しかしながら、二直線\(m,n\)は点\(A\)を交点としているので、これは矛盾しています。

したがって、直線\(m\)以外に、点\(A\)を通り直線\(l\)と交わらない直線\(n\)は引けないことが分かりました。つまり、直線\(m\)、ただ一つのみしか引けません。□

以上で、命題②\( \Rightarrow \)命題④、命題④\( \Rightarrow \)命題③、命題③\( \Rightarrow \)命題②を示しましたので、命題②と命題③と命題④の同値性を示せました。

公開日：２０１９年１２月９日
修正日：ー