東京大学・令和４年第２次前期・数学（理科）第三問の解説と解答

【目次】
０．はじめに
１．解説と解答
　１－１．小問（１）
　１－２．小問（２）
　１－３．小問（３）

はじめに

今回は、過去問の第三回として「東京大学・令和４年（2022年度）第２次前期・数学（理科）第三問」の解説と解答を示します。できるだけ計算や論理に飛躍のないように、くわえて解説も含みますので解答としてはもっと簡潔に記載するようにしてください。誤記・誤答につきましてはご指摘を頂けますと幸いです。

東京大学の著作権保護のため問題文は下記のページよりご確認ください。
https://www.u-tokyo.ac.jp/ja/admissions/undergraduate/e01_04_22.html

解説と解答

第三問は、前々回一般的な受験対策と東京大学・令和４年第２次前期・数学（理科）第一問の解説と解答で解説した通り、まず「教科書に書かれた基本を思い出して問題文の指示に素直に従うこと」、そして解けなければ「何か問題に隠されたアイデアを求めて試行錯誤をしてみる」という取り組み方のうち、第一問と同じで前者によるだけで解ける問題と言えると思います。

くわえて、やはり前々回に指摘しましたが、『数学Ⅱの「図形と方程式」、数学ⅡⅢ「微分法と積分法」は現代科学の屋台骨ですので、必然的にその理解を大学入試でも求められることが多くなる』の通りの典型的な問題と言えるかと思います。そのため、受験問題の中では対策が立てやすく解きやすい問題であると思いますが、他の東京大学の「解きやすい問題」と同様に次のような難しさがあります。

まず、習得を問われる高校数学の教科書（詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください。以下同じ。）の範囲を列挙してみましょう。

中心的に問われる内容：
数学Ⅱ第３章「図形と方程式」第３節「軌跡と領域」９.「不等式の表す領域」
数学Ⅱ第６章「微分法と積分法」第２節「導関数の応用」９.「最大値・最小値」

副次的に問われる内容：
数学Ⅰ第１章「数と式」第１節「式の計算」２.「整式の加法と減法および乗法」
数学Ⅰ第１章「数と式」第３節「１次不等式」７.「１次不等式の利用」Ｂ「絶対値を含む方程式・不等式」
数学Ⅰ第１章「数と式」第２節「実数」５.「根号を含む式の計算」（p.33問題、p.186開平方）
数学Ⅱ第２章「２次関数」第１節「２次方程式と２次不等式」５.「２次方程式」

これらの問題を別々の基本問題として羅列したら３ページ程度にはなるでしょうか。それも『数学Ⅰ第１章「数と式」第１節「式の計算」２.「整式の加法と減法および乗法」』の計算は、面積を式に表すところを含めるとそれなりの量があります。何より問題文を正確に読解し、これらの知識を正確に計算して２０～５０分という短時間で解き切るのは大変なことです。これが他の東京大学の「解きやすい問題」と同様の難しさでしょう。

とはいえ、このように分析すれば東京大学の「解きやすい問題」を解くための理屈は分かります。目標は「問題文を正確に読解し、これらの知識を正確に計算して２０～５０分という短時間で解き切る」ことであり、そのためには教科書をきちんと理解して、基本的な問題演習を積んで、応用問題で読解力や分析力も身に付けていく、という当たり前の勉強法が一番良いということが分かります。

もちろん、受験問題や東京大学の「解きやすい問題」を解くことは勉強の大きな目標ではなく短期的な目標なので、自ずとどのように勉強すれば良いのかという点については様々な観点があり、これらについては前々回の記事や当サイトの内容（特に勉強法）を参考にして頂きたいと思います。

簡単にいえば、知識の習得は大切ですが同時に知識を探求し発見する方法を習得しておくことも大切なことで、どちらが先でどちらが後ということもなく、どちらも一朝一夕でできることでもなく一定の修練が必要なことです。この点、どちらかに偏ることもあり、特に成績の付けやすい前者に偏ることが日本の教育では顕著にみられ、誤解も多い点です。最大の要因は、合理的な学問の伝統が浅いこと、もう一つは受験が画一的だったことによると思います。後者は、一定の公正・平等というメリットもあります。

受験問題は、ある程度の範囲の知識を修得し正確に早く活用できる能力を計るもので、知識を探求し発見する能力を計れるものではありません。前者が得意な人もいれば後者が得意な人もいます。どちらかに偏った能力を持つ人もいますし、バランスの良い人もいます。それ以外にも様々にある自分の適性をある程度は客観的に見ながら努力をし、一喜一憂せず自分の好みと能力を生かせる方向に進むと良いと思います。

それでは、毎回余談が多くなってしまいますがどの程度「教科書をきちんと理解して、基本的な問題演習を積んで、応用問題で読解力や分析力」を身に付けていく必要があるのかを実際に問題を解きながら見て行きましょう。

まずは、一つ一つ確認しながら問題文全体を読んでみるのでした。そうすると、まず座標平面上で「２点が十分離れている」ことの独自の定義が出てきます。これは、教科書の数学Ⅱ第３章「図形と方程式」第３節「軌跡と領域」９.「不等式の表す領域」や数学Ⅰ第１章「数と式」第３節「１次不等式」７.「１次不等式の利用」Ｂ「絶対値を含む方程式・不等式」を理解していれば、特に座標平面上の点と数式を成立させる数の組の対応関係をきちんと理解していれば、絶対値を含む二つの不等式の「または」を次の図のように処理することは難しくありません。

図１：

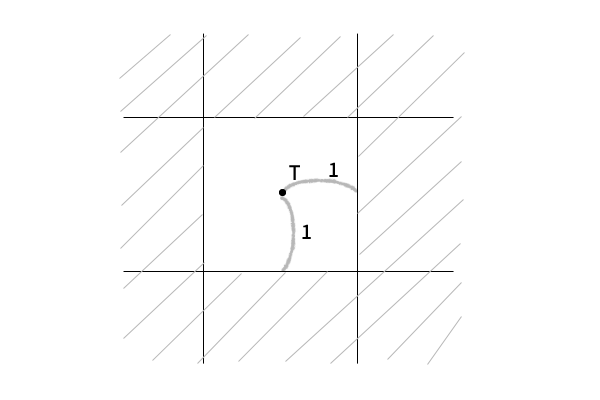
つまり、絶対値を含む二つの不等式のどちらかを成立させる数の組であれば良いので、それに対応する座標平面上の点も二つの不等式が表す領域のどちらかに入っていれば良いということになります。そして、この定義を使いながら領域Ｄ、各点Ｏ、Ａ、Ｂ、Ｐを定義していきます。これを一つ一つ確認しながら次のような図に書き下していきます。

図２：

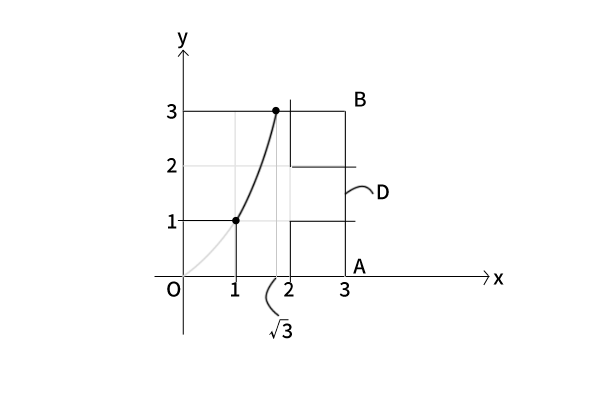
この際に気になるのが\(y=x^2\)が点Ｏ、Ｂとの位置関係でどのような点を通っていくかということですが、点Ｏについては\((1,1)\)を通って十分離れた範囲に出ていき、点Ｂについては\(y=3\)上で\((\sqrt{3},3)\)を通ると分かり、数学Ⅰ第１章「数と式」第２節「実数」５.「根号を含む式の計算」（p.33問題）より\(\sqrt{3}=1.73..\)なので点Ｂから十分離れた範囲を通っていくことが分かります。

ここまで読解してきて小問（１）を読むと、小問（１）はすぐに解けそうだなと感じ、小問（２）小問（３）にも目を通してみます。小問（２）は各点の十分に離れていない領域を領域Ｄから繰り抜いた面積を求める問題だと分かり、小問（３）は点Ｐを動かしたときの最小値をとる\(a\)の位置とあり、順当に解いて行けば数学Ⅱ第６章「微分法と積分法」第２節「導関数の応用」９.「最大値・最小値」で解けそうな問題だなと目途が付きます。

小問（１）

図１より\(1 \leq a \leq \sqrt{3}\)と分かります。

小問（２）

点Ｐの位置に応じて決まる点Ｑの取りうる領域の面積を\(f(a)\)とするのでした。点Ｑの領域は、各点Ｏ、Ａ、Ｂ、Ｐの十分に離れていない領域を領域Ｄから繰り抜いた領域です。そうすると、例えば図３のように点Ｐと各点Ｏ、Ａ、Ｂの十分に離れていない領域は重なり合うことになり、その重なり具合で点Ｑの取りうる領域の形が変わるだろうと予測ができます。

図３：

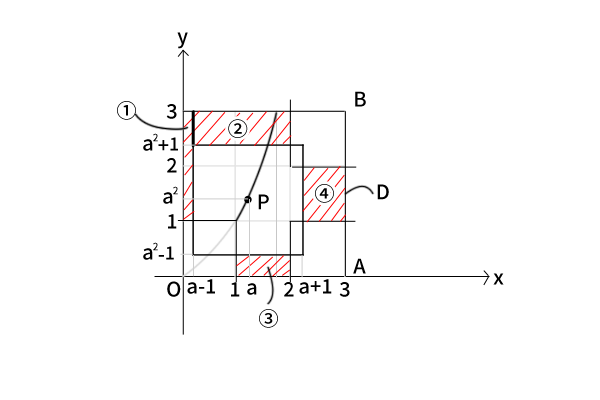
ここで、点Ｑの取りうる領域の面積を\(a\)の計算式で表すわけですが、四角形の面積と円の面積の計算式が異なるように領域の形が変わるにつれ計算式も変えなければならないという幾何学的な理解が必要です。そこで、一般的に適用できる計算式があれば良いのですが、おそらくできないだろう、点Ｐと各点Ｏ、Ａ、Ｂの領域の重なり具合によって形が変わり、それに伴って計算式も変える必要がある、つまり、場合分けが必要だろうと考えます。

そのように考えて、点Ｐを\(1 \leq a \leq \sqrt{3}\)と動かしてみると、まず、明らかに点Ｏ、Ａの領域とは点Ｐが\(y=2\)上に来た時に重なりがなくなることが分かります。一方で、点Ｂの領域とは、一点から始まりずっと領域が重なり続けることが分かります。そこで、以下のように図４を書いてみます。

図４：

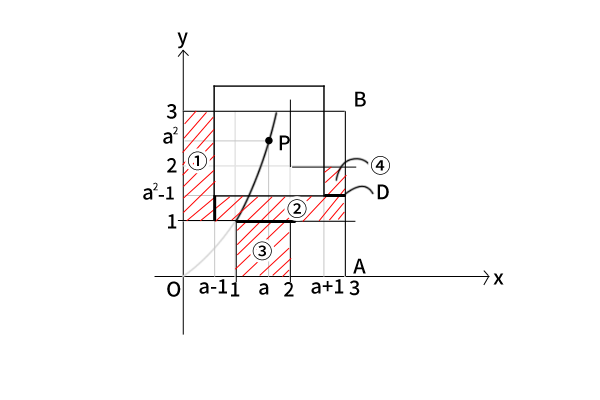
そうして、点Ｑの取りうる領域を図３と図４についてみてみると、点Ｑの取りうる領域を計算のしやすいように四角形に分割した各領域は、図３と図４においてそれぞれ途中で表れたりなくなったり形が四角形から変わったりはしないことを確認できます。つまり、計算式も図３と図４に対応するものを作れば十分と分かります。そこで、点Ｐと点Ｏ、Ａの領域の重なりがなくなる点Ｐが\(y=2\)上に来たところで\(a\)の場合分けをすることにします。つまり、①\(1 \leq a \leq \sqrt{2}\)と②\(\sqrt{2} \leq a \leq \sqrt{3}\)で場合分けをします。

ちなみに、解答例としては以上の考察を詳しく書く必要はなく、\(a\)の場合分けの理由を「点Ｑの取りうる領域が変わるので」と簡潔に述べ図３と図４を書いて対応する\(f(a)\)の計算式を書くだけで良いと思います。時間が余ったときには説明を補足すれば計算間違いした場合の部分点をもらえるかもしれません。

それでは、\(f(a)\)の計算式を書くと、四角形の面積を足し合わせるだけなので一つ一つは難しくはありませんが、焦って書き下すと計算間違いをする恐れがありますので気を付けてください。図に振った番号順に各項が並んでいます。

①\(1 \leq a \leq \sqrt{2}\)、図３の場合：

\[f(a)=(a-1)\cdot 2+\{2-(a-1)\}\{3-(a^2+1)\}+1\cdot (a^2-1)+\{3-(a+1)\}\cdot 1 = a^3-2a^2-a+5\]

②\(\sqrt{2} \leq a \leq \sqrt{3}\)、図４の場合：

\[f(a)=(a-1)\cdot 2+\{(a^2-1)-1\}\cdot \{3-(a-1)\}+1\cdot 1+\{2-(a^2-1)\}\cdot \{3-(a+1)\} = 2a^2+a-3\]

となります。数学Ⅰ第１章「数と式」第１節「式の計算」２.「整式の加法と減法および乗法」の計算が正確に早くできることが求められています。

小問（３）

最小値を取る\(a\)の値を求めるので、数学Ⅱ第６章「微分法と積分法」第２節「導関数の応用」９.「最大値・最小値」であることが分かります。各場合分けについて微分をして関数の増減を調べましょう。

①\(1 \leq a \leq \sqrt{2}\)、図３の場合：

\[f'(a) = 3a^2-4a-1\]

変形して頂点の座標を調べて\(a\)の取りえる範囲での正負を求めても良いのですが、ここでは因数分解ができるかをまず調べて、できないと分かったら数学Ⅱ第２章「２次関数」第１節「２次方程式と２次不等式」５.「２次方程式」の解の公式を使って\(x\)座標との交点を次のように求めます。

\[a = \frac{2\pm \sqrt{7}}{3}\]

ここで\(\sqrt{7}\)の評価ですが、数学Ⅰ第１章「数と式」第２節「実数」５.「根号を含む式の計算」の開平方（p.186）を復習しておいても良いと思いますが、忘れていたとしても普通に「根号を含む式の計算」で絞って行って、\(2.5^2=6.25, 2.7^2=7.29\)なので、（このような四則演算を正確に早くできることも求められていると分かります）

\[2.5 < \sqrt{7} < 2.7 \]

\[\frac{2-2.7}{3} < \frac{2-\sqrt{7}}{3} < \frac{2-2.5}{3},\ \ \frac{2+2.5}{3} < \frac{2+\sqrt{7}}{3} < \frac{2+2.7}{3} \]

\[\frac{-0.7}{3} < \frac{2-\sqrt{7}}{3} < \frac{-0.5}{3},\ \ \frac{4.5}{3} < \frac{2+\sqrt{7}}{3} < \frac{4.7}{3} \]

ここで\(\frac{2-\sqrt{7}}{3} < \frac{-0.5}{3} < 1\)と\(\sqrt{2}\fallingdotseq 1.41 < 1.5 < \frac{2+\sqrt{7}}{3}\)より、

\[\frac{2-\sqrt{7}}{3} < 1 < \sqrt{2} < \frac{2+\sqrt{7}}{3}\]

と分かりました。ここで\(f'(a)\)は下に凸の二次関数なので\(1 \leq a \leq \sqrt{2}\)で負になることが分かりました。したがって、この区間で\(f(a)\)は単調減少することが分かります。

一方、②\(\sqrt{2} \leq a \leq \sqrt{3}\)、図４の場合：

\[f'(a) = 4a+1\]

なので、この区間で正になり\(f(a)\)は単調増加することが分かります。したがって、単調減少から単調増加に切り替わる\(a=\sqrt{2}\)で最小となることが分かりました。

最後に時間があれば、\(f(\sqrt{2})\)を二つの計算式について計算してきちんと一致しているか検算をすると良いと思います。どちらの式でも\(a=\sqrt{2}\)の最小値を計算できるはずなので、よい検算ポイントになります。

公開日：２０２３年４月２６日
修正日：－